Câu hỏi:
65 lượt xem Tự luận
Cho hai tam giác ABC và DEF thỏa mãn AB = DE, AC = DF, = = 60°, BC = 6 cm, = 45°. Tính độ dài cạnh EF và số đo các góc ACB, DEF, EFD
Lời giải
Hướng dẫn giải:
|
GT |
AB = DE, AC = DF, BC = 6 cm, |
|
KL |
Tính EF và số đo các góc ACB, DEF, EFD. |
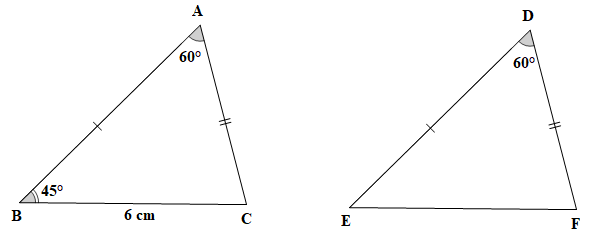
+) Trong tam giác ABC có , theo định lí tổng ba góc trong một tam giác ta có:
Suy ra
Hay
+) Xét tam giác ABC và tam giác DEF có:
AB = DE (theo giả thiết);
(theo giả thiết);
AC = DF (theo giả thiết).
Vậy (c.g.c).
Suy ra: BC = EF (hai cạnh tương ứng) và (các cặp góc tương ứng).
Mà BC = 6 cm; (theo giả thiết) và (chứng minh trên).
Do đó EF = 6 cm;
Vậy EF = 6 cm; và
Câu 2:
Câu 3:
Câu 4:
