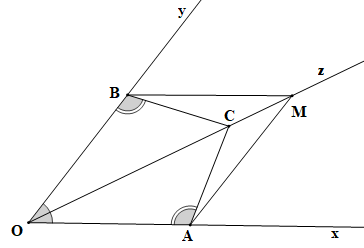
a)

+) Tia Oz là tia phân giác của góc xOy (theo giả thiết) nên $\widehat{xOz}=\widehat{yOz}$ (tính chất tia phân giác của một góc).

 Suy ra $\widehat{AOC}=\widehat{BOC}$.

+) Áp dụng định lí tổng ba góc trong một tam giác cho tam giác OAC và OBC ta có:

Trong tam giác OAC: $\widehat{AOC}+\widehat{OCA}+\widehat{CAO}=180°$ suy ra $\widehat{OCA}=180°-\left(\widehat{AOC}+\widehat{CAO}\right);$

Trong tam giác OBC: $\widehat{BOC}+\widehat{OCB}+\widehat{CBO}=180°$ suy ra $\widehat{OCB}=180°-\left(\widehat{BOC}+\widehat{CBO}\right);$

Mà $\widehat{AOC}=\widehat{BOC}$ (chứng minh trên) và $\widehat{CAO}=\widehat{CBO}$ (theo giả thiết).

Do đó $\widehat{AOC}+\widehat{CAO}$ = $\widehat{BOC}+\widehat{CBO}$.

Suy ra $180°-\left(\widehat{AOC}+\widehat{CAO}\right)=180°-\left(\widehat{BOC}+\widehat{CBO}\right).$

Hay $\widehat{OCA}=\widehat{OCB}$.

+) Xét tam giác OAC và tam giác OBC có:

$\widehat{AOC}=\widehat{BOC}$ (chứng minh trên);

OC là cạnh chung;

$\widehat{OCA}=\widehat{OCB}$ (chứng minh trên).

Vậy $\Delta OAC=\Delta OBC$ (g.c.g).

b) Từ $\Delta OAC=\Delta OBC$ (chứng minh câu a) suy ra OA = OB (hai cạnh tương ứng).

Xét tam giác OAM và tam giác OBM có:

OA = OB (chứng minh trên);

$\widehat{AOM}=\widehat{BOM}$ (do $\widehat{xOz}=\widehat{yOz}$);

OM là cạnh chung.

Vậy $\Delta OAM=\Delta OBM$ (c – g – c)

Do đó, $\widehat{BMO}=\widehat{AMO}$  (hai góc tương ứng) hay $\widehat{BMC}=\widehat{AMC}$

BM = MA (hai cạnh tương ứng)

Xét tam giác MAC và MBC có:

$\widehat{BMC}=\widehat{AMC}$ (chứng minh trên)

BM = MA

CM chung

Vậy $\Delta MAC=\Delta MBC$ (c.g.c).