Cho Hình 4.20, biết AB = CB, AD = CD, góc DAB = 90 độ, góc BDC = 30 độ a) Chứng minh rằng tam giác ABD = tam giác CBD b) Tính góc ABC

Câu hỏi:

37 lượt xem

Tự luận

Cho Hình 4.20, biết AB = CB, AD = CD, $\hat{D A B} = 90 °,$

$\hat{B D C} = 30 ° .$

a) Chứng minh rằng $Δ A B D = Δ C B D .$

b) Tính $\hat{A B C} .$

Xem đáp án

Xem thêm: Giải Toán 7 (Kết nối tri thức) Bài 13: Hai tam giác bằng nhau. Trường hợp bằng nhau thứ nhất của tam giác

Lời giải

Hướng dẫn giải:

$Δ A B D, Δ C B D;$

AB = CB, AD = CD, $\hat{D A B} = 90 °, \hat{B D C} = 30 ° .$

a) $Δ A B D = Δ C B D .$

b) Tính $\hat{A B C} .$

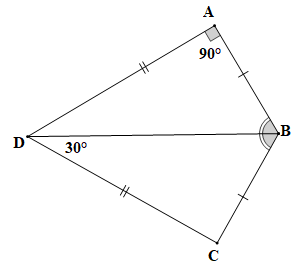
Tài liệu VietJack

a) Chứng minh (hình vẽ trên):

Hai tam giác ABD và CBD có:

AB = CB (theo giả thiết);

AD = CD (theo giả thiết);

BD là cạnh chung.

Vậy $Δ A B D = Δ C B D (c . c . c) .$

b) Vì $Δ A B D = Δ C B D$ (chứng minh câu a)

Nên $\hat{B D A} = \hat{B D C}$ (hai góc tương ứng) và $\hat{A B D} = \hat{C B D}$ (hai góc tương ứng).

Mà $\hat{B D C} = 30 °$ (theo giả thiết), do đó $\hat{B D A} = 30 ° .$

Trong tam giác ABD có $\hat{D A B} = 90 °$ nên là tam giác vuông tại A, khi đó hai góc nhọn của tam giác ABD phụ nhau.

Do đó $\hat{A B D} + \hat{B D A} = 90 ° .$

Suy ra $\hat{A B D} = 90 ° - \hat{B D A}$

$\hat{A B D} = 90 ° - 30 °$

$\hat{A B D} = 60 °$

Tia BD nằm giữa hai tia BA và BC nên $\hat{A B C} = \hat{A B D} + \hat{C B D}$ .

Mà $\hat{A B D} = \hat{C B D}$ (chứng minh trên), do đó $\hat{A B C} = \hat{A B D} + \hat{A B D} .$

Hay $\hat{A B C} = 2 \hat{A B D} = 2.60 ° = 120 ° .$

Vậy $\hat{A B C} = 120 ° .$

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1:

Tự luận

Ta nói hai đoạn thẳng bằng nhau nếu chúng có cùng độ dài, hai góc bằng nhau nếu chúng có cùng số đo góc. Vậy hai tam giác như thế nào thì được gọi là bằng nhau và làm thế nào để kiểm tra được hai tam giác đó bằng nhau

Xem đáp án »

6 tháng trước 28 lượt xem

Câu 2:

Tự luận

Gấp đôi một tờ giấy rồi cắt như Hình 4.9

Xem đáp án »

6 tháng trước 19 lượt xem

Câu 3:

Tự luận

Biết hai tam giác trong Hình 4.11 bằng nhau, em hãy chỉ ra các cặp cạnh tương ứng, các cặp góc tương ứng và viết đúng kí hiệu bằng nhau của cặp tam giác đó

Xem đáp án »

6 tháng trước 20 lượt xem

Câu 4:

Tự luận

Cho tam giác ABC bằng tam giác DEF (H.4.13). Biết rằng BC = 4 cm, $\hat{A B C}$ = 40°, $\hat{A C B}$ = 60°. Hãy tính độ dài đoạn thẳng EF và số đo góc EDF