Câu hỏi:
44 lượt xemLời giải
Hướng dẫn giải:
|
GT |
Đường tròn (O) cắt tia Ox tại A, cắt tia Oy tại B; Đường tròn (A; AO) và đường tròn (B; BO) cắt nhau tại M; Tia Oz đi qua M. |
|
KL |
Tia Oz là tia phân giác của góc xOy. |
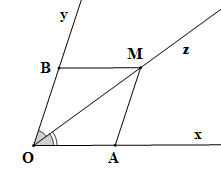
Chứng minh (hình vẽ trên):
Nối BM và AM.
Vì đường tròn (O) cắt tia Ox tại A, cắt tia Oy tại B (theo giả thiết) nên ta có OA = OB.
Đường tròn (A; AO) và đường tròn (B; BO) cắt nhau tại M nên AM = AO và BM = BO.
Mà OA = OB (chứng minh trên).
Do đó AM = BM.
Hai tam giác OAM và OBM có:
OA = OB (chứng minh trên);
AM = BM (chứng minh trên);
OM là cạnh chung.
Vậy
Suy ra (hai góc tương ứng).
Do đó tia Oz là tia phân giác của góc xOy.
Câu 1:
Câu 2:
Câu 3:
Câu 4:
Câu 5:
Câu 6:
Câu 7:
Câu 8:
Câu 10:
Câu 11:
Câu 12:
