Cho hình thang ABCD có cạnh AD vuông góc với hai đáy AB và CD. Số đo góc ở đỉnh B gấp đôi số đo góc ở đỉnh C. Tính số đo các góc của hình thang đó

Question

VietJack · Accepted Answer

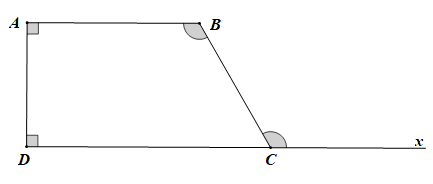
Hướng dẫn giải. GT ABCD là hình thang có hai đáy AB và CD; AD⊥AB,AD⊥CD; ABC^=2BCD^. KL Tính số đo của các góc ABC^,BCD^,CDA^,DAB^. Chứng minh (Hình vẽ trên). ABCD là hình thang có hai đáy là AB và CD nên AB // CD. Vì AD⊥AB tại A nên ta có DAB^=90°. Vì AD⊥CD tại D nên ta có CDA^=90°. Vẽ tia Cx là tia đối của tia CD. Mà AB // CD nên AB // Cx. Từ đó suy ra ABC^=BCx^ (hai góc so le trong). Do CD và Cx là hai tia đối nhau nên BCD^ và BCx^ là hai góc kề bù hay BCD^+BCx^=180° (tính chất hai góc kề bù). Suy ra BCD^+ABC^=180°. Mà ABC^=2BCD^ Nên BCD^+2BCD^=180° 3BCD^=180° BCD^=60° . Suy ra ABC^=2BCD^=2.60°=120°. Vậy ABC^=120°;BCD^=60°;CDA^=90°;DAB^=90°.

Câu hỏi:

Lời giải

Hướng dẫn giải:

ĐỀ THI LIÊN QUAN:

Giới thiệu

Liên kết

Chính sách

Kết nối

Câu hỏi:

Lời giải

Hướng dẫn giải:

ĐỀ THI LIÊN QUAN:

CHỌN BỘ SÁCH BẠN MUỐN XEM