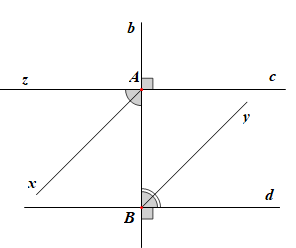
Chứng minh (Hình vẽ trên):

Theo giả thiết $b\perp c$ tại A nên $\widehat{zAB}=90°.$

Do tia Ax là tia phân giác của góc zAB nên Ax nằm giữa hai tia Az và AB; $\widehat{zAx}=\widehat{xAB}=\frac{1}{2}\widehat{zAB}$ (tính chất tia phân giác của một góc).

Mà $\widehat{zAB}=90°$ nên $\widehat{zAx}=\widehat{xAB}=\frac{1}{2}\widehat{zAB}=\frac{1}{2}.90°=45°.\left(1\right)$

Theo giả thiết $b\perp d$ tại B nên $\widehat{ABd}=90°.$

Do tia By là tia phân giác của góc ABd nên tia By nằm giữa hai tia BA và Bd; $\widehat{ABy}=\widehat{yBd}=\frac{1}{2}\widehat{ABd}$ (tính chất tia phân giác của một góc).

Mà $\widehat{ABd}=90°$ nên $\widehat{ABy}=\widehat{yBd}=\frac{1}{2}\widehat{ABd}=\frac{1}{2}.90°=45°.\left(2\right)$

Từ (1) và (2) ta có $\widehat{xAB}=\widehat{ABy}\left(=45°\right).$ 

Mà hai góc này ở vị trí so le trong nên Ax // By (dấu hiệu nhận biết hai đường thẳng song song).

Suy ra đường thẳng chứa tia Ax song song với đường thẳng chứa tia By.

Vậy đường thẳng chứa tia Ax song song với đường thẳng chứa tia By.