Câu hỏi:
101 lượt xemCho hình tứ diện SABC và các điểm A’,B’,C’ lần lượt thuộc các cạnh SA, SB, SC. Giả sử hai đường thẳng B’C’ và BC cắt nhau tại D, hai đường thẳng C’A’ và CA cắt nhau tại E và hai đường thẳng A’B’ và AB cắt nhau tại F. Chứng minh rằng ba điểm D, E, F thẳng hàng.
Lời giải
Hướng dẫn giải:
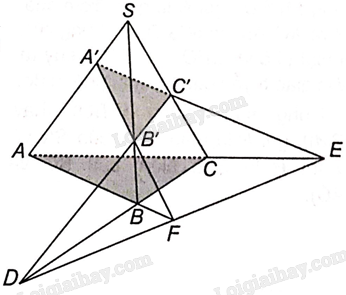
B’C’ và BC cắt nhau tại D nên D nằm trên giao tuyến của hai mặt phẳng (A’B’C’) và (ABC).
C’A’ và CA cắt nhau tại E nên E nằm trên giao tuyến của hai mặt phẳng (A’B’C’) và (ABC).
A’B’ và AB cắt nhau tại F nên F nằm trên giao tuyến của hai mặt phẳng (A’B’C’) và (ABC).
Vậy D, E, F cùng nằm trên giao tuyến của hai mặt phẳng (A’B’C’) và (ABC) nên ba điểm này thẳng hàng.