Câu hỏi:
175 lượt xemCho tam giác ABC cân tại A và M là trung điểm của đoạn thẳng BC. Chứng minh AM vuông góc với BC và AM là tia phân giác của góc BAC
Lời giải
Hướng dẫn giải:
|
GT |
cân tại A, M là trung điểm BC. |
|
KL |
và AM là tia phân giác của góc BAC. |
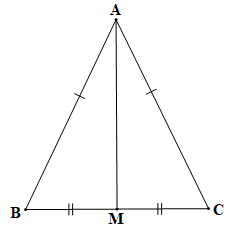
Chứng minh (hình vẽ trên):
Tam giác ABC cân tại A (theo giả thiết) nên AB = AC (định nghĩa tam giác cân).
Xét tam giác ABM và tam giác ACM có:
AB = AC (chứng minh trên);
BM = CM (do M là trung điểm của BC);
AM là cạnh chung.
Vậy (c.c.c).
Suy ra (hai góc tương ứng).
Mà góc AMB và góc AMC là hai góc kề bù nên ta có (tính chất hai góc kề bù).
Do đó .
Suy ra
Từ (chứng minh trên), suy ra (hai góc tương ứng).
Do đó AM là tia phân giác của góc BAC.
Tính số đo các góc và các cạnh chưa biết của tam giác DEF trong Hình 4.62
Sử dụng thước thẳng và compa để vẽ đường trung trực của đoạn thẳng AB như sau
Trong Hình 4.70, đường thẳng nào là đường trung trực của đoạn thẳng AB
