Câu hỏi:
59 lượt xemTam giác vuông có hai cạnh bằng nhau được gọi là tam giác vuông cân.
Hãy giải thích các khẳng định sau:
a) Tam giác vuông cân thì cân tại đỉnh góc vuông;
b) Tam giác vuông cân có hai góc nhọn bằng 45o;
c) Tam giác vuông có một góc nhọn bằng 45o là tam giác vuông cân
Lời giải
Hướng dẫn giải:
a)
|
GT |
|
|
KL |
|
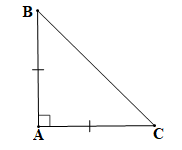
Tam giác ABC vuông tại A nên hai góc nhọn của tam giác phụ nhau suy ra
Khi đó số đo của góc B và góc C sẽ nhỏ hơn 90°.
+) Nếu tam giác ABC cân tại B nên (tính chất tam giác cân).
Mà nên
(vô lí vì
)
Suy ra tam giác ABC vuông tại A thì không thể cân tại B.
+) Nếu tam giác ABC cân tại C nên (tính chất tam giác cân).
Mà nên
(vô lí vì
)
Suy ra tam giác ABC vuông tại A thì không thể cân tại C.
Do vậy tam giác ABC vuông tại A và cân tại A.
b)
|
GT |
|
|
KL |
Hai góc nhọn bằng 45°. |
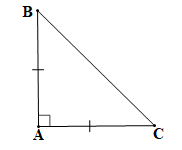
Tam giác ABC vuông cân nên tam giác ABC cân tại đỉnh A (theo câu a).
Suy ra (tính chất tam giác cân).
Mà trong một tam giác vuông, hai góc nhọn phụ nhau nên ta có: .
Do đó
Khi đó
c)
|
GT |
|
|
KL |
|
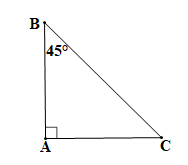
Tam giác ABC vuông tại A (theo giả thiết) nên hai góc nhọn phụ nhau.
Do đó
Suy ra
Khi đó suy ra tam giác ABC cân tại A.
Mà tam giác ABC vuông tại A nên tam giác ABC vuông cân tại A.
Vậy tam giác ABC vuông cân tại A.
Tính số đo các góc và các cạnh chưa biết của tam giác DEF trong Hình 4.62
Sử dụng thước thẳng và compa để vẽ đường trung trực của đoạn thẳng AB như sau
Trong Hình 4.70, đường thẳng nào là đường trung trực của đoạn thẳng AB
