Câu hỏi:
89 lượt xem Tự luận
Cho tứ diện ABCD. Gọi G và H lần lượt là trọng tâm của hai tam giác ABC và ACD. Chứng minh rằng GH//(BCD)
Lời giải
Hướng dẫn giải:
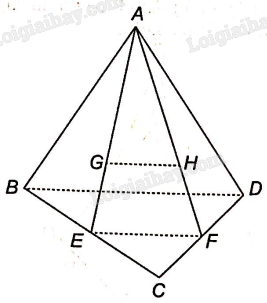
Gọi E, F lần lượt là trung điểm của các cạnh BC, CD. Vì G là trọng tâm của tam giác ABC nên A, G, E thẳng hàng và
Tương tự ta có A, H, F thẳng hàng và
Do đó,
Trong tam giác AEF có: , theo định lí Thalès đảo ta có GH//EF, mà nên GH//(BCD)
Câu 1:
Câu 2:
Câu 6: