Câu hỏi:
78 lượt xemLời giải
Hướng dẫn giải:
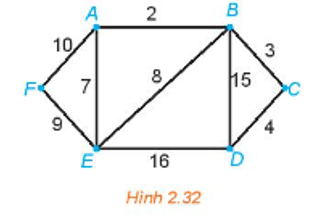
Đồ thị Hình 2.32 chỉ có hai đỉnh bậc lẻ là A và D nên ta có thể tìm được một đường đi Euler từ A đến D (đường đi này đi qua mỗi cạnh đúng một lần).
Một đường đi Euler từ A đến D là AFEABEDBCD và tổng độ dài của nó là
10 + 9 + 7 + 2 + 8 + 16 + 15 + 3 + 4 = 74.
Để quay trở lại điểm xuất phát và có đường đi ngắn nhất, ta cần tìm một đường đi ngắn nhất từ D đến A theo thuật toán gắn nhãn vĩnh viễn.
Đường đi ngắn nhất từ D đến A là DCBA và có độ dài là 4 + 3 + 2 = 9.
Vậy một chu trình cần tìm là AFEABEDBCDCBA và có độ dài là 74 + 9 = 83.
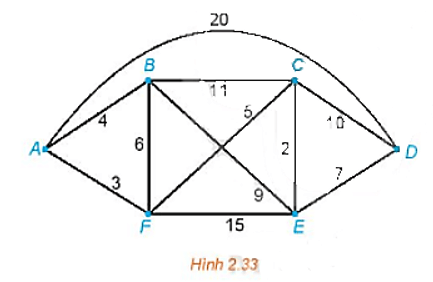
Tìm đường đi ngắn nhất từ A đến D trong đồ thị có trọng số trên Hình 2.33.
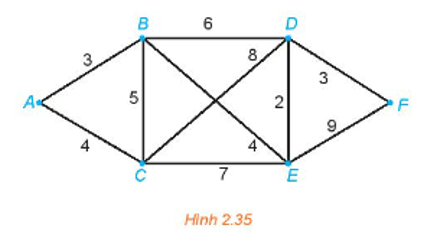
Giải bài toán người đưa thư đối với đồ thị có trọng số trên Hình 2.35.
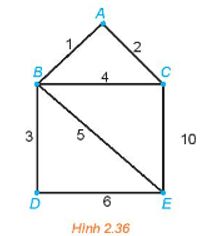
Giải bài toán người đưa thư đối với đồ thị có trọng số trên Hình 2.36.