Câu hỏi:
89 lượt xemLời giải
Hướng dẫn giải:
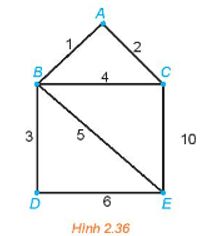
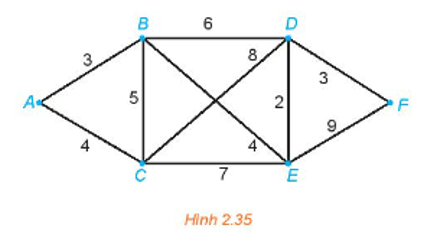
Đồ thị Hình 2.36 chỉ có hai đỉnh bậc lẻ là C và E nên ta có thể tìm được một đường đi Euler từ C đến E (đường đi này đi qua mỗi cạnh đúng một lần).
Một đường đi Euler từ đỉnh C đến đỉnh E là CABCEBDE và tổng độ dài của nó là
2 + 1 + 4 + 10 + 5 + 3 + 6 = 31.
Để quay trở lại điểm xuất phát và có đường đi ngắn nhất, ta cần tìm một đường đi ngắn nhất từ E đến C theo thuật toán gắn nhãn vĩnh viễn.
Đường đi ngắn nhất từ E đến C là EBAC và có độ dài là 5 + 1 + 2 = 8.
Vậy một chu trình cần tìm là CABCEBDEBAC và có độ dài là 31 + 8 = 39.
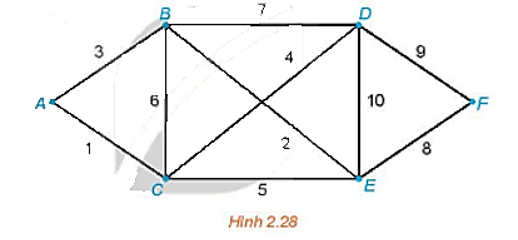
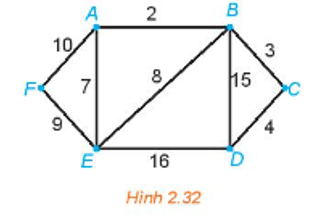
Giải bài toán người đưa thư đối với đồ thị có trọng số trên Hình 2.32.
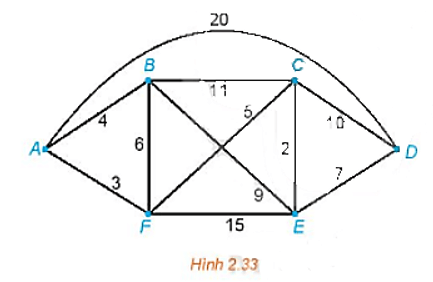
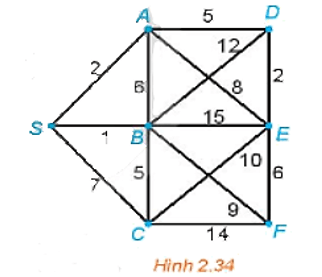
Tìm đường đi ngắn nhất từ A đến D trong đồ thị có trọng số trên Hình 2.33.
Giải bài toán người đưa thư đối với đồ thị có trọng số trên Hình 2.35.