Câu hỏi:
45 lượt xem Tự luận
Gọi AI và AM lần lượt là đường cao và đường trung tuyến xuất phát từ đỉnh A của tam giác ABC. Chứng minh rằng:
a) AI < (AB + AC);
b) AM < (AB + AC)
Lời giải
Hướng dẫn giải:
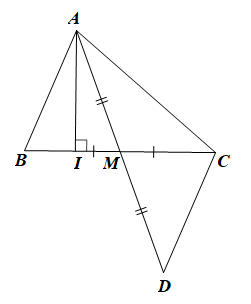
a) Xét AIC vuông tại I có AC là cạnh huyền.
Do đó AC > AI (1).
Xét AIB vuông tại I có AB là cạnh huyền.
Do đó AB > AI (2).
Từ (1) và (2) ta có AB + AC > AI + AI hay AB + AC > 2AI
Suy ra AI <
b) Lấy D sao cho M là trung điểm của AD.
Xét ABM và DCM có:
MA = MD (theo cách vẽ),
(hai góc đối đỉnh),
MB = MC (do M là trung điểm của BC),
Do đó ABM = DCM (c.g.c)
Suy ra AB = DC (hai cạnh tương ứng).
Khi đó AB + AC = DC + AC.
Trong ACD có DC + AC > AD (bất đẳng thức tam giác)
Hay AB + AC > AD.
Mà AD = 2AM (do M là trung điểm của AD).
Suy ra AB + AC > 2AM hay AM < (AB + AC).
Vậy AM < (AB + AC).
Câu 1:
Câu 2:
Câu 4:
