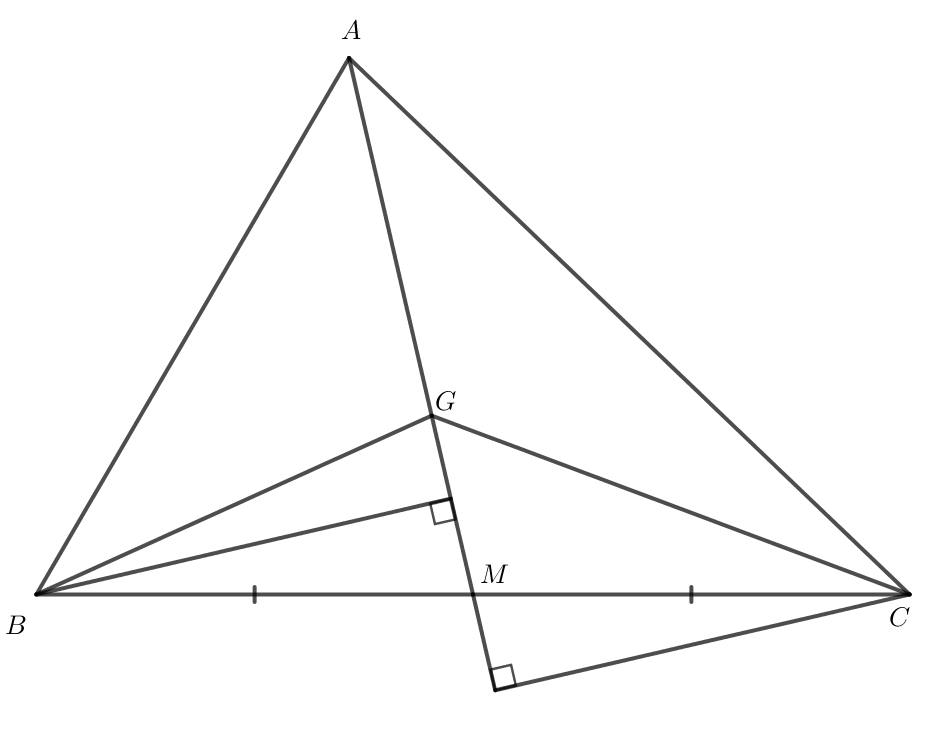
a) Do G là trọng tâm của tam giác ABC và M là trung điểm của BC nên GM = $\frac{1}{3}$AM.

$∆$ABM và $∆$MBG có chung đường cao kẻ từ B đến AM nên tỉ số diện tích giữa MBG và $∆$ABM bằng tỉ số của hai đáy GM và AM.

Ta có GM = $\frac{1}{3}$AM nên S_MBG = $\frac{1}{3}$S_ABM.

$∆$ACM và $∆$MCG có chung đường cao kẻ từ C đến AM nên tỉ số diện tích giữa $∆$MCG và $∆$ACM bằng tỉ số của hai đáy GM và AM.

Ta có GM = $\frac{1}{3}$AM nên S_MCG = $\frac{1}{3}$S_ACM.

Do đó S_MBG + S_MCG = $\frac{1}{3}$S_ABM + $\frac{1}{3}$S_ACM

Hay S_GBC = $\frac{1}{3}$(S_ABM + S_ACM) = $\frac{1}{3}$S_ABC.

b) Chứng minh tương tự câu a:

Do G là trọng tâm của $∆$ABC nên AG = 2GM suy ra S_GCA = 2S_MCG; S_GAB = 2S_MBG.

Do BC = 2MB = 2MC nên S_GBC = 2S_MCG = 2S_MBG.

Do đó S_GCA = S_GAB = S_GBC = $\frac{1}{3}$S_ABC.