Câu hỏi:
79 lượt xemMột công ty sau khi tăng giá 30 nghìn đồng mỗi sản phẩm so với giá ban đầu là 2x (nghìn đồng) thì có doanh thu là 6x2 + 170x + 1 200 (nghìn đồng). Tính số sản phẩm mà công ty đó đã bán được theo x
Lời giải
Hướng dẫn giải:
Giá sản phẩm ban đầu là 2x (nghìn đồng)
Sau khi tăng giá 30 nghìn đồng thì giá sản phẩm lúc này là 2x + 30 (nghìn đồng).
Doanh thu là 6x2 + 170x + 1 200 (nghìn đồng), do đó số sản phẩm mà công ty đó bán được là: (6x2 + 170x + 1 200) : (2x + 30)
Thực hiện phép chia đa thức ta được:
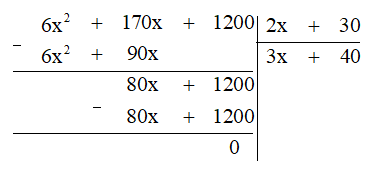
Khi đó (6x2 + 170x + 1 200) : (2x + 30) = 3x + 40.
Vậy công ty đó đã bán được 3x + 40 sản phẩm.
Thực hiện phép chia:
a) (2x2 + 5x + 2) : (2x + 1);
b) (3x3 - 5x2 + 2) : (x2 + 1)
