Câu hỏi:
89 lượt xemMột hình hộp chữ nhật có thể tích là x3 + 6x2 + 11x + 6 (cm3). Biết đáy là hình chữ nhật có các kích thước là x + 1 (cm) và x + 2 (cm). Tính chiều cao của hình hộp chữ nhật đó theo x
Lời giải
Hướng dẫn giải:
Đáy của hình hộp chữ nhật là hình chữ nhật có các kích thước là x + 1 (cm) và x + 2 (cm) nên diện tích đáy của hình hộp chữ nhật là:
(x + 1).(x + 2) = x.x + x.2 + 1.x + 1.2 = x2 + 2x + x + 2 = x2 + 3x + 2 (cm2).
Hình hộp chữ nhật có thể tích là x3 + 6x2 + 11x + 6 (cm3) nên chiều cao của hình hộp chữ nhật là: (x3 + 6x2 + 11x + 6) : (x2 + 3x + 2)
Thực hiện phép chia đa thức ta được:
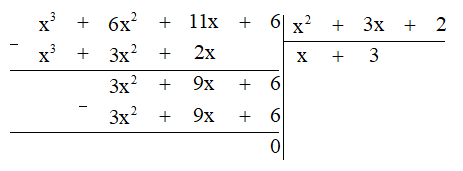
Khi đó (x3 + 6x2 + 11x + 6) : (x2 + 3x + 2) = x + 3.
Vậy chiều cao của hình hộp chữ nhật đó là x + 3 cm.
Thực hiện phép chia:
a) (2x2 + 5x + 2) : (2x + 1);
b) (3x3 - 5x2 + 2) : (x2 + 1)
