Câu hỏi:
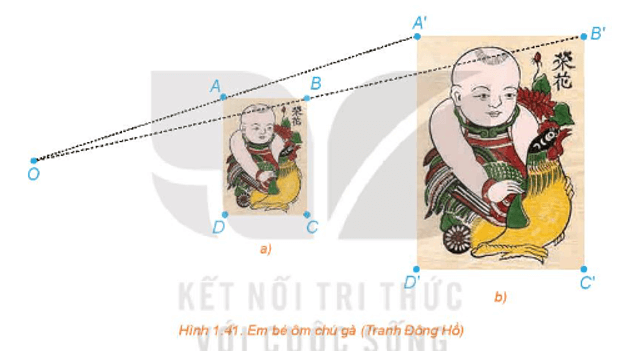
61 lượt xemHĐ1 trang 26 Chuyên đề Toán 11: Trong hai bức tranh ở Hình 1.41, các hình chữ nhật ABCD, A'B'C'D' có các cạnh tương ứng song song, bức tranh lớn có kích thước gấp đôi bức tranh nhỏ.
a) Giải thích vì sao các đường thẳng AA', BB', CC', DD' cùng đi qua một điểm O.
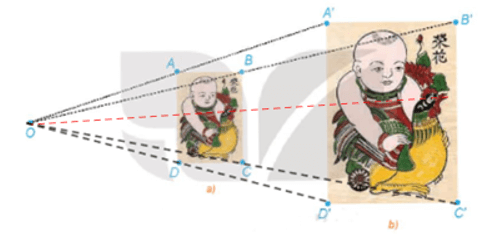
b) Hãy tính các tỉ số .
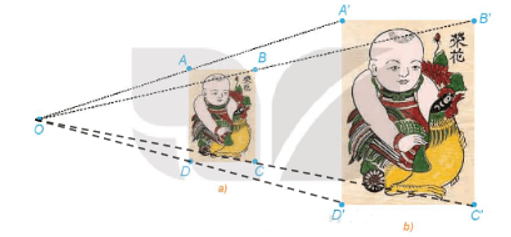
c) Dùng thước thẳng nối hai điểm tương ứng nào đó trên hai bức tranh (chẳng hạn, đầu mỏ trên của chú gà ở hai bức tranh). Đường thẳng đó có đi qua O hay không?
Lời giải
Hướng dẫn giải:
a) Gọi O là giao điểm của AA' và BB'.
Xét tam giác OA'B' có AB // A'B', theo định lý Thales, ta có:
.
Từ đó suy ra A, B lần lượt là trung điểm của OA' và OB'.
Gọi C' là giao điểm của BC và OC'. Vì BC // B'C' nên BC' // B'C'.
Xét tam giác OB'C' có BC' // B'C' và B là trung điểm của OB' nên BC' là đường trung bình của tam giác OB'C'. Suy ra BC' = B'C' và C' là trung điểm của OC'.
Mặt khác theo giả thiết ta có BC = B'C'. Do vậy C' trùng với C và C là trung điểm của OC'.
Chứng minh tương tự, ta được D là trung điểm của OD'.
Vậy các đường thẳng AA', BB', CC', DD' cùng đi qua một điểm O.
b) Vì A, B, C, D lần lượt là trung điểm của OA', OB', OC', OD' nên
.
c) Dùng thước thẳng nối hai điểm tương ứng trên hai bức tranh, cụ thể, đầu mỏ trên của chú gà ở hai bức tranh, ta thấy đường thẳng này đi qua điểm O.
ĐỀ THI LIÊN QUAN:
-
34 câu hỏi 78 lượt thi