Giáo án PowerPoint Bài 1: Giới hạn của dãy số (Cánh diều 2024) | Bài giảng điện tử Toán 11

I. MỤC TIÊU:

1. Kiến thức, kĩ năng:Học xong bài này, HS đạt các yêu cầu sau:

- Nhận biết được khái niệm giới hạn của dãy số.

- Giải thích được một số giới hạn cơ bản như: $\underset{n\to +\infty }{lim}\frac{1}{n^k}=0(k\in {\mathbb{N}}^{*}),\underset{n\to +\infty }{lim}{q}^n=0\left(\right|q|<1)$ và $\underset{n\to +\infty }{lim}c=c$ với c là hằng số.

- Vận dụng được các giới hạn cơ bản và các phép toán giới hạn dãy số để tìm giới hạn của một số dãy số đơn giản (ví dụ: $\underset{n\to +\infty }{lim}\frac{2n+1}{n};\underset{n\to +\infty }{lim}\frac{\sqrt{4n^2+1}}{n}$)

- Tính được tổng của một cấp số nhân lùi vô hạn và vận dụng được kết quả đó để giải quyết một số tình huống thực tiễn giả định hoặc liên quan đến thực tiễn.

2. Năng lực

Năng lực chung:

- Năng lực tự chủ và tự học trong tìm tòi khám phá

- Năng lực giao tiếp và hợp tác trong trình bày, thảo luận và làm việc nhóm

- Năng lực giải quyết vấn đề và sáng tạo trong thực hành, vận dụng.

Năng lực riêng:

- Tư duy và lập luận toán học: phát hiện được điểm tương đồng và khác biệt để nhận biết hàm số; chỉ ra chứng cứ, lập luận để khẳng định $limc=c,lim\frac{6n+1}{n}=6,...$

- Mô hình hóa toán học: sử dụng số hạng dãy số $\left(u_n\right)$ để biểu thị cho khối lượng chất phóng xạ còn lại sau chu kì thứ n,....

- Giải quyết vấn đề toán học: xác định được cách thức để chứng minh dãy số có giới hạn hữu hạn, hoặc $lim{n}^3=+\infty$,...

- Giao tiếp toán học: đọc hiểu thông tin toán học từ đồ thị.

- Sử dụng công cụ, phương tiện học toán.

3. Phẩm chất

- Có ý thức học tập, ý thức tìm tòi, khám phá và sáng tạo, có ý thức làm việc nhóm, tôn trọng ý kiến các thành viên khi hợp tác.

- Chăm chỉ tích cực xây dựng bài, có trách nhiệm, chủ động chiếm lĩnh kiến thức theo sự hướng dẫn của GV.

II. THIẾT BỊ DẠY HỌC VÀ HỌC LIỆU

1. Đối với GV: SGK, Tài liệu giảng dạy, giáo án, đồ dùng dạy học.

2. Đối với HS: SGK, SBT, vở ghi, giấy nháp, đồ dùng học tập (bút, thước...), bảng nhóm, bút viết bảng nhóm.

III. TIẾN TRÌNH DẠY HỌC

A. HOẠT ĐỘNG KHỞI ĐỘNG (MỞ ĐẦU)

a) Mục tiêu:

− Tạo hứng thú, thu hút HS tìm hiểu nội dung bài học.

b) Nội dung: HS đọc tình huống mở đầu, suy nghĩ trả lời câu hỏi.

c) Sản phẩm: HS trả lời được câu hỏi mở đầu.

d) Tổ chức thực hiện:

Bước 1: Chuyển giao nhiệm vụ:

− GV yêu cầu HS đọc tình huống mở đầu:

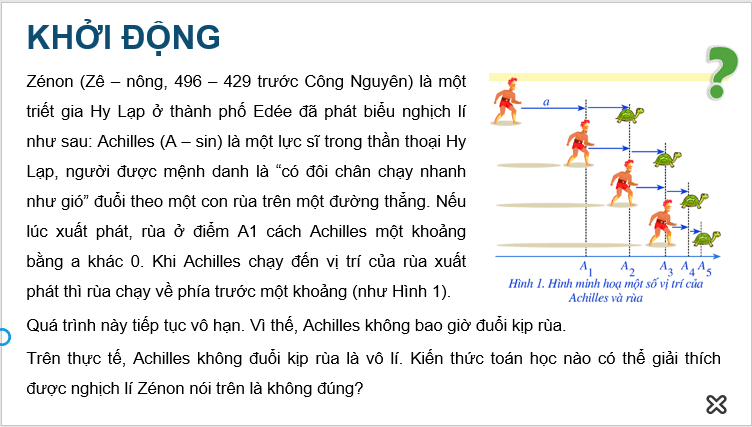
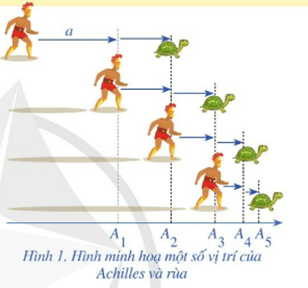
Zénon (Zê – nông, 496 – 429 trước Công Nguyên) là một triết gia Hy Lạp ở thành phố Edée đã phát biểu nghịch lí như sau: Achilles (A – sin) là một lực sĩ trong thần thoại Hy Lạp, người được mệnh danh là “có đôi chân chạy nhanh như gió” đuổi theo một con rùa trên một đường thẳng. Nếu lúc xuất phát, rùa ở điểm A1 cách Achilles một khoảng bằng a khác 0. Khi Achilles chạy đến vị trí của rùa xuất phát thì rùa chạy về phía trước một khoảng (như Hình 1). Quá trình này tiếp tục vô hạn. Vì thế, Achilles không bao giờ đuổi kịp rùa.

Trên thực tế, Achilles không đuổi kịp rùa là vô lí. Kiến thức toán học nào có thể giải thích được nghịch lí Zénon nói trên là không đúng?

Bước 2: Thực hiện nhiệm vụ: HS quan sát và chú ý lắng nghe, thảo luận nhóm đôi hoàn thành yêu cầu.

Bước 3: Báo cáo, thảo luận: GV gọi một số HS trả lời, HS khác nhận xét, bổ sung.

Bước 4: Kết luận, nhận định: GV đánh giá kết quả của HS, trên cơ sở đó dẫn dắt HS vào bài học mới:

“Trong chương này, chúng ta sẽ tìm hiểu về một phép toán mới: phép toán giới hạn. Nhờ phép toán này, người ta xây dựng nên những khái niệm cơ bản của Giải tích toán học như tính liên tục, đạo hàm và tích phân. Nội dung của chương này gồm: giới hạn của dãy số, giới hạn của hàm số và tính liên tục của hàm số. Để tìm đáp án cho câu hỏi trên, chúng ta vào bài học tìm hiểu về giới hạn của hàm số.”

Bài 1. Giới hạn của dãy số

B. HÌNH THÀNH KIẾN THỨC MỚI

Hoạt động 1: Giới hạn hữu hạn của dãy số

a) Mục tiêu:

− HS nhận biết được khái niệm giới hạn 0 và giới hạn hữu hạn của dãy số.

− Giải thích được một số giới hạn cơ bản như: $lim\frac{1}{n^k}=0(k\in {\mathbb{N}}^{*}),lim{q}^n=0\left(\right|q|<1)$ và lim c = c với c là hằng số.

− HS vận dụng được các giới hạn cơ bản và các phép toán giới hạn dãy số để tìm giới hạn của một số dãy số.

................................

................................

................................