Câu hỏi:
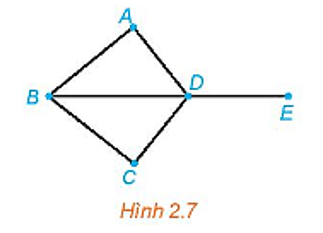
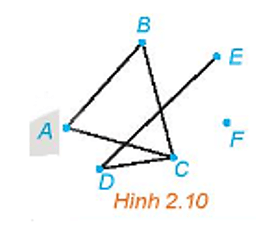
30 lượt xemCho đồ thị như Hình 2.7. Bằng cách đi dọc theo các cạnh, với điều kiện không đi qua cạnh nào quá một lần (có thể có cạnh không cần đi qua), hãy chỉ ra các cách để:
a) Đi từ đỉnh A đến đỉnh E.
b) Đi từ đỉnh A và lại quay về đỉnh A.
Lời giải
Hướng dẫn giải:
a) Để đi từ đỉnh A đến đỉnh E ta có thể di chuyển theo con đường từ A đến D rồi từ D đến E (hoặc cũng có thể chọn các con đường khác, chẳng hạn đi theo đường từ A đến B rồi từ B đến D và từ D đến E, ...)
b) Để đi từ đỉnh A và lại quay về đỉnh A ta có thể di chuyển theo con đường từ A đến D rồi từ D đến B và từ B quay lại A (tương tự cũng có thể chọn các con đường khác).
Cho đồ thị như Hình 2.5. Tìm các đỉnh là đầu mút của: 0 cạnh; 1 cạnh; 2 cạnh; 3 cạnh.
Chứng minh rằng một đồ thị đầy đủ có n đỉnh thì có n(n−1)2𝑛𝑛−12 cạnh.
Chứng minh rằng không tồn tại đồ thị với các đỉnh có bậc là 2, 3, 3, 4, 4 và 5.
ĐỀ THI LIÊN QUAN:
-
34 câu hỏi 78 lượt thi