Câu hỏi:
98 lượt xem Tự luận
Hãy vẽ một đồ thị có 4 đỉnh và:
a) có đúng hai đỉnh cùng bậc và bậc là 1;
b) có đúng hai đỉnh cùng bậc và bậc là 2.
Lời giải
Hướng dẫn giải:
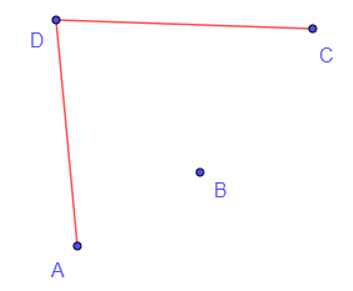
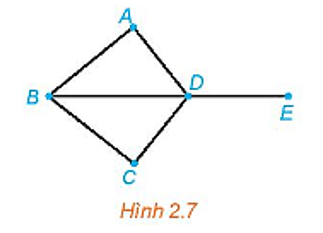
a) Đồ thị có 4 đỉnh và có đúng hai đỉnh cùng bậc và bậc là 1.
Ở đây, đỉnh A và C đều có bậc 1, trong khi đỉnh D có bậc 2, còn đỉnh B có bậc 0.
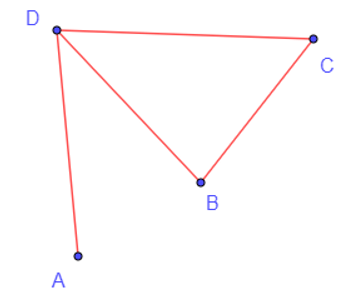
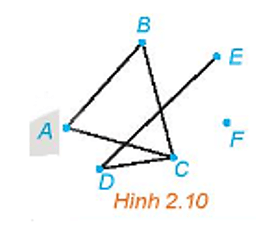
b) Đồ thị có 4 đỉnh và có đúng hai đỉnh cùng bậc và bậc là 2.
Ở đây, đỉnh B và C đều có bậc 2, trong khi đỉnh D có bậc 3, còn đỉnh A có bậc 1.
Câu 4:
Câu 5:
Câu 6:
Câu 7:
Câu 8:
Câu 9:
Câu 10:
Câu 11:
Câu 12:
Câu 13:
Câu 14:
Câu 16:
Câu 17:
Tự luận
Chứng minh rằng một đồ thị đầy đủ có n đỉnh thì có n(n−1)2??−12 cạnh.
1 năm trước
85 lượt xem
Câu 18:
Tự luận
Chứng minh rằng không tồn tại đồ thị với các đỉnh có bậc là 2, 3, 3, 4, 4 và 5.
1 năm trước
97 lượt xem