Câu hỏi:
84 lượt xemLời giải
Hướng dẫn giải:
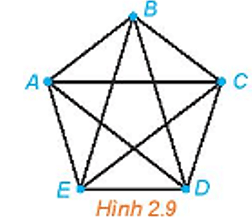
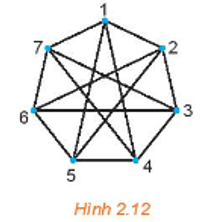
Do đồ thị đầy đủ nên mỗi đỉnh được nối với n – 1 đỉnh khác, tức là số cạnh là n(n – 1) cạnh.
Tuy nhiên, do ở trên ta đã tính lặp một cạnh 2 lần, nên số cạnh thực tế của đồ thị là n(n−1)2??−12.
Câu 4:
Câu 5:
Câu 6:
Câu 7:
Câu 8:
Câu 9:
Câu 10:
Câu 11:
Câu 12:
Câu 13:
Câu 14:
Câu 15:
Câu 16:
Câu 18:
Tự luận
Chứng minh rằng không tồn tại đồ thị với các đỉnh có bậc là 2, 3, 3, 4, 4 và 5.
1 năm trước
95 lượt xem