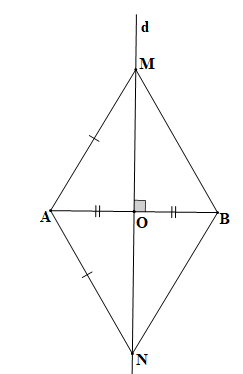
M và N là hai điểm phân biệt nằm trên đường trung trực của AB với AM = AN nên M và N có vị trí như hình vẽ trên.

Gọi O là giao điểm của AB và MN, d là đường trung trực của AB nên $d\perp AB$ tại trung điểm O của AB.

Xét tam giác OAM (vuông tại O) và tam giác OAN (vuông tại O) có:

OA là cạnh chung;

AM = AN (theo giả thiết).

Vậy $\Delta OAM=\Delta OAN$ (cạnh huyền – cạnh góc vuông).

Suy ra OM = ON (hai cạnh tương ứng) và $\widehat{AMO}=\widehat{ANO}$ (hai góc tương ứng).

Xét tam giác OBM (vuông tại O) và tam giác OBN (vuông tại O) có:

OB là cạnh chung;

OM = ON (chứng minh trên).

Vậy $\Delta OBM=\Delta OBN$ (hai cạnh góc vuông).

Suy ra MB = NB (hai cạnh tương ứng) và $\widehat{BMO}=\widehat{BNO}$ (hai góc tương ứng).

Ta có $\widehat{AMO}=\widehat{ANO}$ (chứng minh trên) và $\widehat{BMO}=\widehat{BNO}$ (chứng minh trên) nên $\widehat{AMO}+\widehat{BMO}=\widehat{ANO}+\widehat{BNO}.$

Mà $\widehat{AMB}=\widehat{AMO}+\widehat{BMO}$ và $\widehat{ANB}=\widehat{ANO}+\widehat{BNO}.$

Suy ra $\widehat{AMB}=\widehat{ANB}.$