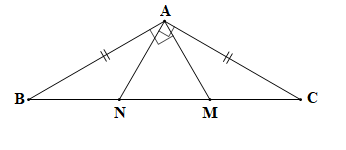
a) Tam giác ABC cân tại A (theo giả thiết) nên AB = AC và $\widehat{B}=\widehat{C}$.

$MA\perp AB$ tại A (theo giả thiết) nên $\widehat{BAM}=90°;$ $NA\perp AC$ tại A (theo giả thiết) nên $\widehat{NAC}=90°;$

Xét tam giác BAM (vuông tại A) và tam giác CAN (vuông tại A) có:

AB = AC (chứng minh trên);

$\widehat{B}=\widehat{C}$ (chứng minh trên).

Vậy $\Delta BAM=\Delta CAN$ (cạnh góc vuông – góc nhọn kề).

b) Trong tam giác ABC có $\widehat{A}+\widehat{B}+\widehat{C}=180°$ (định lí tổng ba góc trong một tam giác).

Suy ra $\widehat{B}+\widehat{C}=180°-\widehat{A}$.

Mà $\widehat{A}=120°$ (theo giả thiết) và $\widehat{B}=\widehat{C}$ (chứng minh trên).

Do đó $\widehat{B}+\widehat{B}=180°-120°$

$2\widehat{B}=60°$ 

$\widehat{B}=30°$ 

Khi đó $\widehat{B}=\widehat{C}=30°.$        (1)

Ta có: $\widehat{BAM}<\widehat{BAC}$ (do 90° < 120°) nên tia AM nằm giữa hai tia AB và AC.

Do đó $\widehat{BAC}=\widehat{BAM}+\widehat{MAC}$.

Suy ra $\widehat{MAC}=\widehat{BAC}-\widehat{BAM}=120°-90°=30°$.   

Vậy $\widehat{MAC}=30°.$            (2)

Tương tự ta cũng có $\widehat{BAC}=\widehat{BAN}+\widehat{NAC}$.

Suy ra $\widehat{BAN}=\widehat{BAC}-\widehat{NAC}=120°-90°=30°.$ 

Vậy $\widehat{BAN}=30°$.            (3)

Từ (1), (2) và (3) ta có: $\widehat{B}=\widehat{C}=\widehat{MAC}=\widehat{BAN}\left(=30°\right).$

Do đó tam giác ABN cân tại N (do $\widehat{B}=\widehat{BAN}$);

Và tam giác ACM cân tại M (do $\widehat{C}=\widehat{MAC}$).