Câu hỏi:
156 lượt xemCho tam giác ABC. Ba đường trung tuyến AM, BN, CP đồng quy tại G. Chứng minh:
GA + GB + GC = (AM + BN + CP)
Lời giải
Hướng dẫn giải:
|
GT |
DABC, ba đường trung tuyến AM, BN, CP đồng quy tại G |
|
KL |
GA + GB + GC = (AM + BN + CP). |
Chứng minh (Hình vẽ dưới đây):
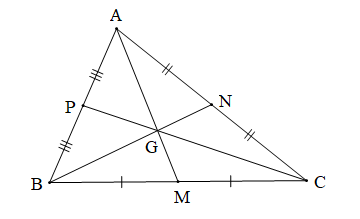
Tam giác ABC có ba đường trung tuyến AM, BN, CP đồng quy tại G nên G là trọng tâm của tam giác ABC.
Khi đó AG = AM; BG = BN; CG = CP (tính chất trọng tâm của tam giác)
Do đó GA + GB + GC = AM + BN + CP = (AM + BN + CP).
Vậy GA + GB + GC = (AM + BN + CP).
Quan sát Hình 97 và cho biết các đầu mút của đoạn thẳng AM có đặc điểm gì.
Trong Hình 101, đoạn thẳng HK là đường trung tuyến của những tam giác nào?
Quan sát các đường trung tuyến AM, BN, CP của tam giác ABC trong Hình 104.
