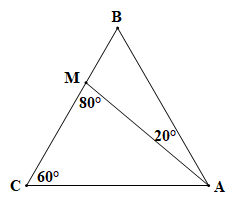
Chứng minh (hình vẽ trên):

+) Điểm M nằm trên cạnh BC nên tia MB là tia đối của tia MC, khi đó góc AMC và góc AMB là hai góc kề bù.

Do đó $\widehat{AMB}+\widehat{AMC}=180°$ (tính chất hai góc kề bù).

Suy ra $\widehat{AMB}=180°-\widehat{AMC}$ 

$\widehat{AMB}=180°-80°=100°$

Vậy $\widehat{AMB}=100°.$ 

+) Xét tam giác AMB có góc AMC là góc ngoài của tam giác tại đỉnh M, do đó $\widehat{AMC}=\widehat{ABM}+\widehat{BAM}$ (tính chất góc ngoài của một tam giác).

Suy ra $\widehat{ABM}=\widehat{AMC}-\widehat{BAM}$

$\widehat{ABM}=80°-20°$

$\widehat{ABM}=60°.$ 

Do đó $\widehat{ABC}=\widehat{ABM}=60°.$ 

Vậy $\widehat{ABC}=60°.$

+) Áp dụng định lí tổng ba góc trong một tam giác cho tam giác ABC với $\widehat{ABC}=60°,$ $\widehat{BCA}=60°$ ta có: $\widehat{BAC}+\widehat{ABC}+\widehat{BCA}=180°$

Suy ra $\widehat{BAC}=180°-\widehat{ABC}-\widehat{BCA}$ 

Hay $\widehat{BAC}=180°-60°-60°$

$\widehat{BAC}=60°.$ 

Vậy $\widehat{BAC}=60°.$ 

​