Chứng minh (Hình vẽ dưới đây):

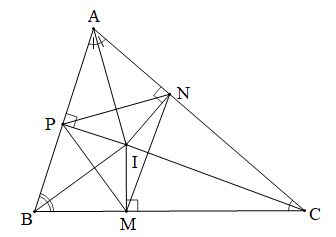
Do M, N, P lần lượt là hình chiếu của I trên các cạnh BC, CA, AB (giả thiết)

Nên IM $\perp$ BC, IN $\perp$AC, IP $\perp$ AB.

Vì I là giao điểm của ba đường phân giác (giả thiết)

Nên IM = IN = IP (tính chất giao điểm ba đường phân giác)

+) Chứng minh IA là đường trung trực của đoạn thẳng NP.

Vì IN = IP (chứng minh trên) nên I thuộc đường trung trực của NP (1)

Xét $∆$API (vuông tại P) và $∆$ANI (vuông tại N) có:

AI là cạnh chung,

IP = IN (chứng minh trên)

Do đó $∆$API = $∆$ANI (cạnh huyền - cạnh góc vuông).

Suy ra AP = AN (hai cạnh tương ứng).

Do đó A thuộc đường trung trực của NP (2)

Từ (1) và (2) suy ra IA là đường trung trực của NP.

+) Chứng minh IB là đường trung trực của PM.

Vì IP = IM (chứng minh trên) nên I thuộc đường trung trực của PM. (3)

Xét $∆$BMI (vuông tại M) và $∆$BPI (vuông tại P) có:

BI là cạnh chung,

IM = IP (chứng minh trên)

Do đó $∆$BMI = $∆$BPI (cạnh huyền - cạnh góc vuông).

Suy ra BM = BP (hai cạnh tương ứng).

Do đó B thuộc đường trung trực của PM. (4)

Từ (3) và (4) suy ra IB là đường trung trực của PM.

+) Chứng minh IC là đường trung trực của MN.

Vì IM = IN (chứng minh trên) nên I thuộc đường trung trực của MN. (5)

Xét $∆$CMI (vuông tại M) và $∆$CNI (vuông tại N) có:

CI là cạnh chung,

IM = IN (chứng minh trên).

Do đó $∆$CMI = $∆$CNI (cạnh huyền - cạnh góc vuông).

Suy ra CM = CN (hai cạnh tương ứng).

Do đó C thuộc đường trung trực của MN. (6)

Từ (5) và (6) suy ra IC là đường trung trực của MN.