Câu hỏi:
191 lượt xemLời giải
Hướng dẫn giải:
|
GT |
ABC, I là giao điểm của ba đường phân giác |
|
KL |
a) ; b) . |
Chứng minh (Hình vẽ dưới đây):
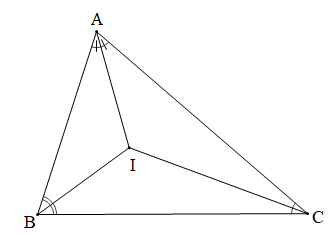
a) Vì AI là đường phân giác của nên (tính chất tia phân giác của một góc)
Vì BI là đường phân giác của nên (tính chất tia phân giác của một góc)
Vì CI là đường phân giác của nên (tính chất tia phân giác của một góc)
Suy ra
Xét tam giác ABC ta có (tổng ba góc của một tam giác)
Do đó .
Vậy
b) Vì CI là đường phân giác của nên .
Suy ra .
Do đó .
Xét tam giác BIC có: (tổng ba góc của một tam giác)
Do đó .
Vậy
Câu 1:
Câu 2:
Câu 3:
Câu 4:
Câu 5:
Câu 6:
Câu 7:
Câu 8:
Câu 10:
