Câu hỏi:
91 lượt xemTam giác ABC có ba đường phân giác cắt nhau tại I. Gọi M, N, P lần lượt là hình chiếu của I trên các cạnh BC, CA, AB
Lời giải
Hướng dẫn giải:
|
GT |
ABC, I là giao điểm của ba đường phân giác, M, N, P lần lượt là hình chiếu của I trên các cạnh BC, CA, AB |
|
KL |
a) IMN, INP, IPM có là tam giác cân không? Vì sao? b) ANP, BPM, CMN có là tam giác cân không? Vì sao? |
Chứng minh (Hình vẽ dưới đây):
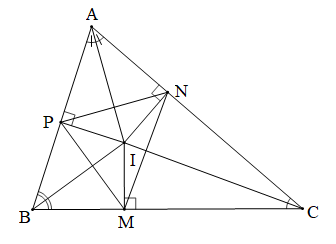
a) Do M, N, P lần lượt là hình chiếu của I trên các cạnh BC, CA, AB (giả thiết)
Nên IM BC, IN AC, IP AB.
Vì I là giao điểm của ba đường phân giác (giả thiết)
Nên IM = IN = IP (tính chất giao điểm ba đường phân giác)
Vì IM = IN nên IMN cân tại I.
Vì IN = IP nên INP cân tại I.
Vì IP = IM nên IPM cân tại I.
b) +) Xét API (vuông tại P) và ANI (vuông tại N) có:
AI là cạnh chung,
IP = IN (chứng minh trên)
Do đó API = ANI (cạnh huyền - cạnh góc vuông).
Suy ra AP = AN (hai cạnh tương ứng).
Tam giác ANP có AP = AN nên tam giác ANP cân tại A.
+) Xét BMI (vuông tại M) và BPI (vuông tại P) có:
BI là cạnh chung,
IM = IP (chứng minh trên)
Do đó BMI = BPI (cạnh huyền - cạnh góc vuông).
Suy ra BM = BP (hai cạnh tương ứng).
Tam giác BPM có BP = BM nên tam giác BPM cân tại B.
+) Xét CMI (vuông tại M) và CNI (vuông tại N) có:
CI là cạnh chung,
IM = IN (chứng minh trên).
Do đó CMI = CNI (cạnh huyền - cạnh góc vuông).
Suy ra CM = CN (hai cạnh tương ứng).
Tam giác CMN có CM = CN nên tam giác CMN cân tại C.
Tam giác ABC có ba đường phân giác cắt nhau tại I. Chứng minh:
a) ;
b)
