Câu hỏi:
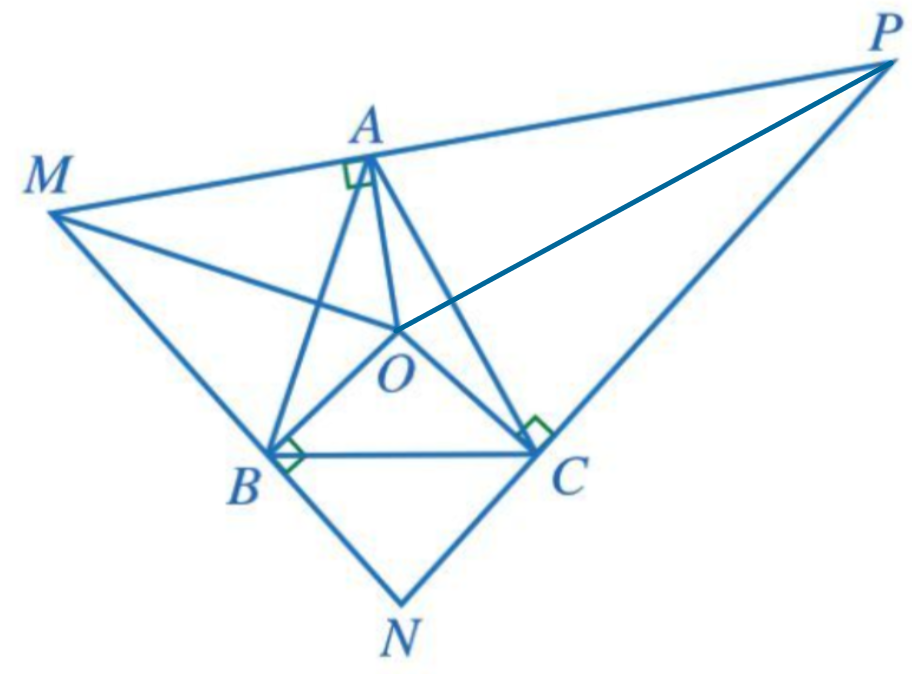
106 lượt xemCho tam giác ABC có O là giao điểm của ba đường trung trực. Qua các điểm A, B, C lần lượt kẻ các đường thẳng vuông góc với OA, OB, OC, hai trong ba đường đó lần lượt cắt nhau tại M, N, P (Hình 144)
Lời giải
Hướng dẫn giải:
|
GT |
MP |
|
KL |
a) b) O là giao điểm ba đường phân giác của tam giác MNP. |
Chứng minh (Hình 144):
a) Vì O là giao điểm ba đường trung trực của tam giác ABC nên OA = OB = OC.
Xét OAM (vuông tại A) và
OBM (vuông tại B) có:
OM là cạnh chung,
OA = OB (chứng minh trên),
Do đó OAM =
OBM (cạnh huyền - cạnh góc vuông).
Suy ra (hai góc tương ứng).
Khi đó MO là tia phân giác của hay MO là tia phân giác của
.
Vậy tia MO là tia phân giác của
b) Nối OP (Hình vẽ dưới đây):
Xét OAP (vuông tại A) và
OCP (vuông tại C) có:
OP là cạnh chung,
OA = OC (chứng minh trên),
Do đó OAP =
OCP (cạnh huyền - cạnh góc vuông).
Suy ra (hai góc tương ứng).
Khi đó PO là tia phân giác của hay PO là tia phân giác của
.
Trong một tam giác, ba đường phân giác của tam giác đó luôn cùng đi qua một điểm
Mà O là giao điểm hai đường phân giác của góc và góc
, do đó O là giao điểm ba đường phân giác của tam giác MNP.
Vậy O là giao điểm ba đường phân giác của tam giác MNP.
Cho tam giác ABC có:
a) Tính .
b) So sánh độ dài các cạnh AB, BC, CA
Cho tam giác nhọn MNP có trực tâm H. Khi đó, góc HMN bằng góc nào sau đây
