Câu hỏi:
74 lượt xemCho tam giác ABC và điểm M thuộc cạnh BC thoả mãn ∆AMB = ∆AMC (Hình 32).
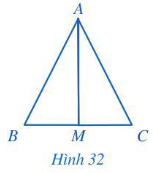
Chứng minh rằng:
a) M là trung điểm của đoạn thẳng BC;
b) Tia AM là tia phân giác của góc BAC và
Lời giải
Hướng dẫn giải:
|
GT |
DABC, M ∈ BC ∆AMB = ∆AMC. |
|
KL |
a) M là trung điểm của BC; b) Tia AM là tia phân giác của góc BAC và |
Chứng minh (Hình 32):
a) Vì ∆AMB = ∆AMC (giả thiết) nên ta có: MB = MC (hai cạnh tương ứng)
Suy ra M là trung điểm của BC.
b) Vì ∆AMB = ∆AMC (giả thiết) nên ta có:
+) (hai góc tương ứng) do đó tia AM là tia phân giác của góc BAC;
+) (hai góc tương ứng)
Lại có và là hai góc kề bù nên: (tính chất hai góc kề bù)
Suy ra
Hay
Do đó
Suy ra
Vậy tia AM là tia phân giác của góc BAC và
Cho biết ∆ABC = ∆MNP, AC = 4 cm, =45°. Tính độ dài cạnh MP và số đo góc ACB
Cho biết ∆PQR = ∆IHK, = 71°, = 49°. Tính số đo góc K của tam giác IHK