Câu hỏi:
54 lượt xemChứng minh rằng:
a) Trong một tam giác cân, hai đường trung tuyến ứng với hai cạnh bên là hai đoạn thẳng bằng nhau.
b) Ngược lại, nếu tam giác có hai đường trung tuyến bằng nhau thì tam giác đó cân
Lời giải
Hướng dẫn giải:
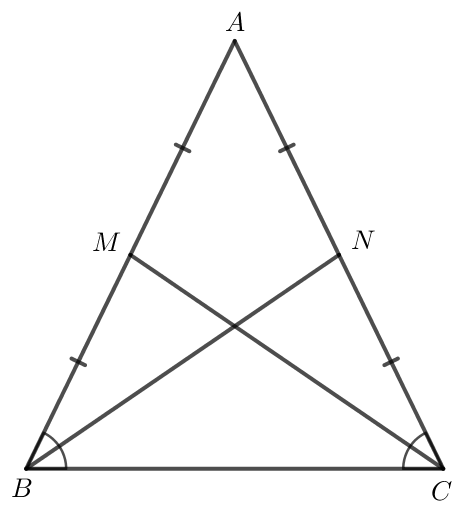
Giả sử ABC cân tại A có M, N lần lượt là trung điểm của AB và AC.
a) Do ABC cân tại A nên AB = AC và (tính chất tam giác cân).
Vì M là trung điểm của AB nên AM = AB;
Vì N là trung điểm của AC nên AN = AC.
Mà AB = AC nên AM = AN
Xét ANB và AMC có:
AM = AN (chứng minh trên).
là góc chung
AB = AC (chứng minh trên).
Suy ra ANB = AMC (c.g.c).
Do đó BN = MC (hai cạnh tương ứng).
Vậy trong một tam giác cân, hai đường trung tuyến ứng với hai cạnh bên là hai đoạn thẳng bằng nhau.
b) Giả sử ABC có hai trung tuyến CM, BN bằng nhau và cắt nhau tại G.
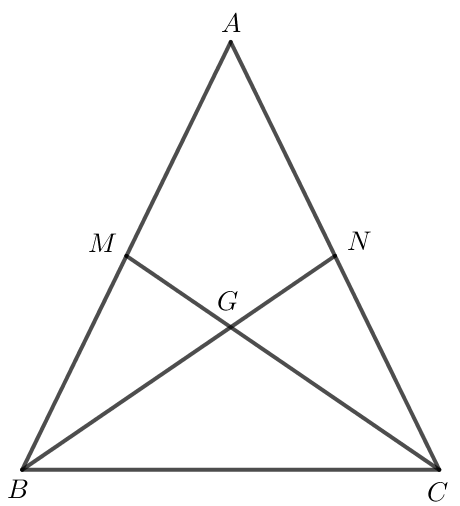
Vì G là giao điểm của hai đường trung tuyến BN và CM của tam giác ABC nên G là trọng tâm tam giác ABC.
Do đó CG = CM, BG = BN.
Mà CM = BN (giả thiết) nên CG = BG.
BGC có CG = BG nên BGC cân tại G.
Suy ra (tính chất tam giác cân)
Xét BMC và CNB có:
MC = NB (theo giả thiết),
(do ),
BC là cạnh chung.
Do đó BMC = CNB (c.g.c).
Suy ra (hai góc tương ứng).
DABC có nên ABC cân tại A.
Vậy nếu tam giác có hai đường trung tuyến bằng nhau thì tam giác đó cân.
Trong tam giác ABC ở Ví dụ 1, cho trung tuyến BN và GN = 1 cm. Tính GB và NB
Gọi BE và CF là hai đường phân giác của tam giác ABC cân tại A. Chứng minh BE = CF
