Câu hỏi:
114 lượt xemChứng minh rằng trong tam giác đều, điểm cách đều ba cạnh của tam giác là trọng tâm của tam giác đó
Lời giải
Hướng dẫn giải:
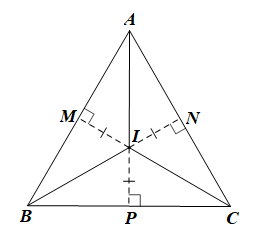
Giả sử ABC đều có điểm I cách đều ba cạnh của tam giác, tức IM = IN = IP (hình vẽ).
Khi đó điểm I là giao điểm của ba đường phân giác của tam giác ABC.
Do ABC đều nên ABC cũng cân tại A.
Theo kết quả Ví dụ 2, trang 75, ta có AI là đường trung tuyến của ABC.
Chứng minh tương tự, ta cũng có:
• ABC đều nên ABC cân tại B, do đó BI là đường trung tuyến của ABC;
• ABC đều nên ABC cân tại C, do đó CI là đường trung tuyến của ABC.
Suy ra AI, BI, CI là ba đường trung tuyến của ABC cắt nhau tại điểm I.
Khi đó I là trọng tâm của tam giác ABC.
Vậy trong tam giác đều, điểm cách đều ba cạnh của tam giác là trọng tâm của tam giác đó.
Trong tam giác ABC ở Ví dụ 1, cho trung tuyến BN và GN = 1 cm. Tính GB và NB
Gọi BE và CF là hai đường phân giác của tam giác ABC cân tại A. Chứng minh BE = CF
