Câu hỏi:
85 lượt xemTrong tam giác ABC, hai đường phân giác của các góc B và C cắt nhau tại D. Kẻ DP vuông góc với BC, DQ vuông góc với CA, DR vuông góc với AB
Lời giải
Hướng dẫn giải:
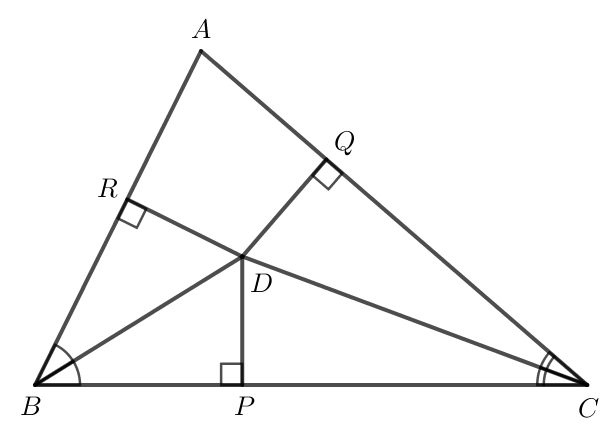
a) Vì D nằm trên tia phân giác BD của góc ABC nên D cách đều hai cạnh BA và BC.
Do đó DR = DP.
b) Vì D nằm trên tia phân giác CD của góc ACB nên D cách đều hai cạnh CB và CA.
Do đó DP = DQ.
c) Từ câu a và b ta có DR = DP và DQ = DP nên DR = DQ.
Ta có D nằm trong góc BAC và D cách đều hai cạnh AB và AC của góc BAC nên D nằm trên tia phân giác của góc BAC.
Vậy D nằm trên tia phân giác của góc BAC.
Trong tam giác ABC ở Ví dụ 1, cho trung tuyến BN và GN = 1 cm. Tính GB và NB
