Câu hỏi:
116 lượt xemHĐ2 trang 7 Toán 11 Tập 1: Nhận biết hệ thức Chasles
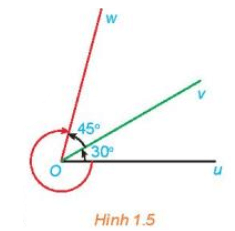
Cho ba tia Ou, Ov, Ow với số đo của các góc hình học uOv và vOw lần lượt là 30° và 45°.
a) Xác định số đo của ba góc lượng giác (Ou, Ov), (Ov, Ow) và (Ou, Ow) được chỉ ra ở Hình 1.5.
b) Với các góc lượng giác ở câu a, chứng tỏ rằng có một số nguyên k để
sđ(Ou, Ov) + sđ(Ov, Ow) = sđ(Ou, Ow) + k360°.
Lời giải
Hướng dẫn giải:
Lời giải:
a) Quan sát Hình 1.5 ta có:
sđ(Ou, Ov) = 30°;
sđ(Ov, Ow) = 45°;
sđ(Ou, Ow) = – (360° – 30° – 45°) = – 285°.
b) Ta có: sđ(Ou, Ov) + sđ(Ov, Ow) = 30° + 45° = 75°.
Lại có: – 285° + 1 . 360° = 75°.
Vậy tồn tại một số nguyên k = 1 để sđ(Ou, Ov) + sđ(Ov, Ow) = sđ(Ou, Ow) + k360°.