Câu hỏi:
105 lượt xemTính:
a) (x2 + 2x + 3) + (3x2 - 5x + 1);
b) (4x3 - 2x2 - 6) - (x3 - 7x2 + x - 5);
c) -3x2(6x2 - 8x + 1);
d) (4x2 + 2x + 1)(2x - 1);
e) (x6 - 2x4 + x2) : (-2x2);
g) (x5 - x4 - 2x3) : (x2 + x)
Lời giải
Hướng dẫn giải:
a) (x2 + 2x + 3) + (3x2 - 5x + 1)
= x2 + 2x + 3 + 3x2 - 5x + 1
= (x2 + 3x2) + (2x - 5x) + (3 + 1)
= (1 + 3)x2 + (2 – 5)x + 4
= 4x2 - 3x + 4.
b) (4x3 - 2x2 - 6) - (x3 - 7x2 + x - 5)
= 4x3 - 2x2 - 6 - x3 + 7x2 - x + 5
= (4x3 - x3) + (-2x2 + 7x2) - x + (-6 + 5)
= (4 – 1)x3 + (‒2 + 7)x2 – x ‒ 1
= 3x3 + 5x2 - x - 1.
c) -3x2(6x2 - 8x + 1)
= -3x2.6x2 - (-3x2).8x + (-3x2).1
= (-3).6.x2+2 – (–3).8.x2+1 + (–3).1.x2
= -18x4 - (-24)x3 + (-3)x2
= - 18x4 + 24x3 - 3x2.
d) (4x2 + 2x + 1)(2x - 1)
= 4x2.2x - 4x2.1 + 2x.2x - 2x.1 + 1.2x - 1.1
= 4.2.x2+1 - 4.1.x2 + 2.2.x1+1 - 2x + 2x - 1
= 8x3 - 4x2 + 4x2 + (-2x + 2x) - 1
= 8x3 + (-4x2 + 4x2) - 1
= 8x3 - 1.
e) (x6 - 2x4 + x2) : (-2x2)
= x6 : (-2x2) - 2x4 : (-2x2) + x2 : (-2x2)
=
=
g) Thực hiện phép chia đa thức ta được:
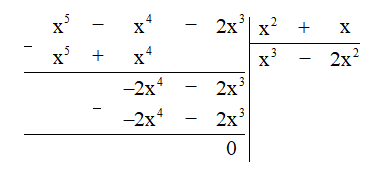
Vậy (x5 - x4 - 2x3) : (x2 + x) = x3 - 2x2.
Tính:
a) -2x2 + 6x2;
b) 4x3 - 8x3;
c) 3x4(-6x2);
d) (-24x6) : (-4x3)
