Câu hỏi:
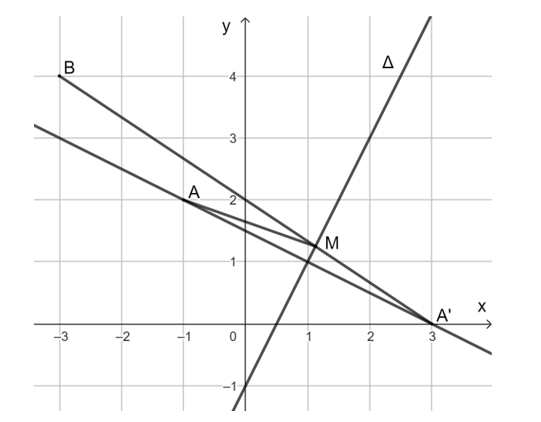
537 lượt xemBài 1.27 trang 33 Chuyên đề Toán 11: Trong mặt phẳng tọa độ Oxy, cho đường thẳng ∆: 2x – y – 1 = 0 và hai điểm A(– 1; 2), B(– 3; 4).
a) Tìm tọa độ điểm A' là ảnh của điểm A qua phép đối xứng trục ∆.
b) Xác định điểm M thuộc đường thẳng ∆ sao cho MA + MB đạt giá trị nhỏ nhất.
Lời giải
Hướng dẫn giải:
a) Ta có: 2 . (– 1) – 2 – 1 = – 5 ≠ 0 nên A(– 1; 2) không thuộc ∆.
Gọi H là chân đường vuông góc hạ từ A xuống ∆.
Vì H thuộc ∆ nên H(x; 2x – 1). Ta có: , vectơ chỉ phương của đường thẳng ∆ là .
Vì AH vuông góc với ∆ nên .
Từ đó suy ra x = 1 nên H(1; 1).
Vì A' là ảnh của điểm A qua phép đối xứng trục ∆ nên AA' vuông góc với ∆ tại H và H là trung điểm của AA'. Suy ra . Vậy A'(3; 0).
b)
Ta có: 2 . (– 3) – 4 – 1 = – 11; 2 . (– 1) – 2 – 1 = – 5 và (– 11) . (– 5) = 55 > 0 nên hai điểm A và B nằm về một phía của đường thẳng ∆.
Vì M thuộc ∆ và A và A' đối xứng nhau qua ∆ nên MA = MA' và A' và B nằm về hai phía của đường thẳng ∆.
Do đó, MA + MB = MA' + MB đạt giá trị nhỏ nhất khi M là giao điểm của A'B và ∆.
Ta có: , suy ra là một vectơ pháp tuyến của đường thẳng A'B. Phương trình đường thẳng A'B là 2(x – 3) + 3(y – 0) = 0 hay 2x + 3y – 6 = 0.
Tọa độ giao điểm M của A'B và ∆ là nghiệm của hệ phương trình . Vậy .