Giải chuyên đề Toán 11 (Kết nối tri thức) Bài tập cuối chuyên đề 1

Giải Chuyên đề Toán 11 Bài tập cuối chuyên đề 1

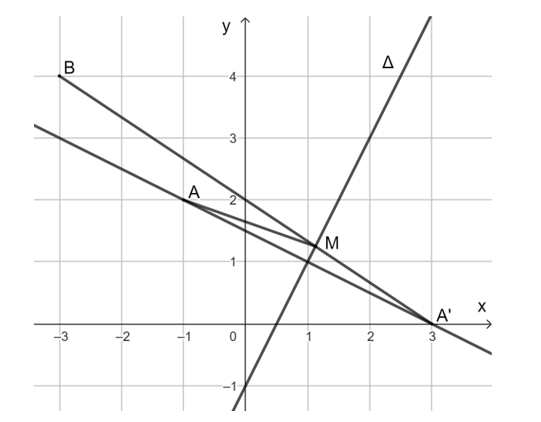
Bài 1.27 trang 33 Chuyên đề Toán 11: Trong mặt phẳng tọa độ Oxy, cho đường thẳng ∆: 2x – y – 1 = 0 và hai điểm A(– 1; 2), B(– 3; 4).

a) Tìm tọa độ điểm A' là ảnh của điểm A qua phép đối xứng trục ∆.

b) Xác định điểm M thuộc đường thẳng ∆ sao cho MA + MB đạt giá trị nhỏ nhất.

Lời giải:

a) Ta có: 2 . (– 1) – 2 – 1 = – 5 ≠ 0 nên A(– 1; 2) không thuộc ∆.

Gọi H là chân đường vuông góc hạ từ A xuống ∆.

Vì H thuộc ∆ nên H(x; 2x – 1). Ta có: $\overrightarrow{AH}=\left(x+1;2x-3\right)$, vectơ chỉ phương của đường thẳng ∆ là $\overrightarrow{u_{\Delta }}=\left(1;2\right)$.

Vì AH vuông góc với ∆ nên $\overrightarrow{AH}.\overrightarrow{u_{\Delta }}=0\iff \left(x+1\right).1+\left(2x-3\right).2=0$.

Từ đó suy ra x = 1 nên H(1; 1).

Vì A' là ảnh của điểm A qua phép đối xứng trục ∆ nên AA' vuông góc với ∆ tại H và H là trung điểm của AA'. Suy ra $\left\{\begin{array}{l}{x}_{A\text{'}}=2x_H-x_A=2.1-\left(-1\right)=3\\ y_{A\text{'}}=2y_H-y_A=2.1-2=0\end{array}\right.$. Vậy A'(3; 0).

b)

Ta có: 2 . (– 3) – 4 – 1 = – 11; 2 . (– 1) – 2 – 1 = – 5 và (– 11) . (– 5) = 55 > 0 nên hai điểm A và B nằm về một phía của đường thẳng ∆.

Vì M thuộc ∆ và A và A' đối xứng nhau qua ∆ nên MA = MA' và A' và B nằm về hai phía của đường thẳng ∆.

Do đó, MA + MB = MA' + MB đạt giá trị nhỏ nhất khi M là giao điểm của A'B và ∆.

Ta có: $\overrightarrow{A\text{'}B}=\left(-6;4\right)$, suy ra $\overrightarrow{n_{A\text{'}B}}=\left(2;3\right)$ là một vectơ pháp tuyến của đường thẳng A'B. Phương trình đường thẳng A'B là 2(x – 3) + 3(y – 0) = 0 hay 2x + 3y – 6 = 0.

Tọa độ giao điểm M của A'B và ∆ là nghiệm của hệ phương trình $\left\{\begin{array}{l}2x-y-1=0\\ 2x+3y-6=0\end{array}\right.$ $\iff \left\{\begin{array}{l}x=\frac{9}{8}\\ y=\frac{5}{4}\end{array}\right.$. Vậy $M\left(\frac{9}{8};\frac{5}{4}\right)$.

Bài 1.28 trang 33 Chuyên đề Toán 11: Trong mặt phẳng tọa độ Oxy, cho đường thẳng d: 2x – y + 5 = 0. Viết phương trình đường thẳng d' là ảnh của đường thẳng d qua phép tịnh tiến theo vectơ $\overrightarrow{u}\left(-3;4\right)$.

Lời giải:

Cách 1:

Lấy A(0; 5), B(1; 7) thuộc đường thẳng d.

Gọi A', B' tương ứng là ảnh của A, B qua phép tịnh tiến theo vectơ $\overrightarrow{u}\left(-3;4\right)$

Khi đó: $\overrightarrow{AA\text{'}}=\overrightarrow{u}$và $\overrightarrow{BB\text{'}}=\overrightarrow{u}$. Suy ra A'(– 3; 9) và B'(– 2; 11).

Vì đường thẳng d' là ảnh của đường thẳng d qua phép tịnh tiến theo vectơ $\overrightarrow{u}\left(-3;4\right)$ nên hai điểm A', B' thuộc đường thẳng d'.

Ta có: $\overrightarrow{A\text{'}B\text{'}}=\left(1;2\right)$, suy ra đường thẳng d' có một vectơ pháp tuyến là $\overrightarrow{n}=\left(2;-1\right)$.

Phương trình đường thẳng d' là 2(x + 3) – (y – 9) = 0 hay 2x – y + 15 = 0.

Cách 2:

Gọi M(x; y) thuộc đường thẳng d và M'(x'; y') là ảnh của điểm M qua phép tịnh tiến theo vectơ $\overrightarrow{u}\left(-3;4\right)$. Khi đó $\overrightarrow{MM\text{'}}=\overrightarrow{u}$ $\iff \left\{\begin{array}{l}x\text{'}-x=-3\\ y\text{'}-y=4\end{array}\right.\iff \left\{\begin{array}{l}x=x\text{'}+3\\ y=y\text{'}-4\end{array}\right.$.

Ta có M thuộc ∆ ⇔ 2x – y + 5 = 0 ⇔ 2(x' + 3) – (y' – 4) + 5 = 0 ⇔ 2x' – y' + 15 = 0. Do đó, M'(x'; y') thuộc đường thẳng có phương trình 2x – y + 15 = 0.

Vì đường thẳng d' là ảnh của đường thẳng d qua phép tịnh tiến theo vectơ $\overrightarrow{u}\left(-3;4\right)$ nên M' thuộc đường thẳng d'.

Vậy phương trình đường thẳng d' là 2x – y + 15 = 0.

Bài 1.29 trang 33 Chuyên đề Toán 11: Trong mặt phẳng tọa độ Oxy, cho đường tròn (C): x2 + y2 – 2x – 4y – 4 = 0. Viết phương trình của đường tròn (C') là ảnh của đường tròn (C) qua phép đối xứng tâm A(3; – 3)

Lời giải:

Ta có (C): x2 + y2 – 2x – 4y – 4 = 0 hay x2 + y2 – 2 . 1 x – 2 . 2 y – 4 = 0.

Suy ra đường tròn (C) có tâm I(1; 2) và bán kính R = $\sqrt{1^2+2^2-\left(-4\right)}=3$.

Gọi I' và R' lần lượt là tâm và bán kính của đường tròn (C'). Vì (C') là ảnh của (C) qua phép đối xứng tâm A(3; – 3) nên I' là ảnh của I qua phép đối xứng tâm A(3; – 3) và R' = R = 3.

Vì I' là ảnh của I qua phép đối xứng tâm A nên A là trung điểm của II'.

Suy ra $\left\{\begin{array}{l}{x}_{I\text{'}}=2x_A-x_I=2.3-1=5\\ y_{I\text{'}}=2y_A-y_I=2.\left(-3\right)-2=-8\end{array}\right.$ nên I'(5; – 8).

Vậy phương trình đường tròn (C') là

(x – 5)2 + [y – (– 8)]2 = 32 hay (x – 5)2 + (y + 8)2 = 9.

Bài 1.30 trang 33 Chuyên đề Toán 11: Trong mặt phẳng tọa độ Oxy, cho đường tròn (C): (x – 1)2 + (y + 2)2 = 9. Phép vị tự tâm O(0; 0) với tỉ số k = – 2 biến đường tròn (C) thành đường tròn (C'). Viết phương trình đường tròn (C').

Lời giải:

Ta có (C): (x – 1)2 + (y + 2)2 = 9 hay (x – 1)2 + [y – (– 2)]2 = 32.

Suy ra đường tròn (C) có tâm I(1; – 2) và bán kính R = 3.

Gọi I' và R' lần lượt là tâm và bán kính của đường tròn (C'). Vì (C') là ảnh của (C) qua phép vị tự tâm O(0; 0) với tỉ số k = – 2 nên I' là ảnh của I qua phép vị tự tâm O(0; 0) với tỉ số k = – 2 và R' = |– 2|.R = 2 . 3 = 6.

Vì I' là ảnh của I qua phép vị tự V(O, – 2) nên $\overrightarrow{OI\text{'}}=-2\overrightarrow{OI}$.

Suy ra $\left\{\begin{array}{l}{x}_{I\text{'}}=-2x_I=-2.1=-2\\ y_{I\text{'}}=-2y_I=-2.\left(-2\right)=4\end{array}\right.$ nên I'(– 2; 4).

Vậy phương trình đường tròn (C') là

[x – (– 2)]2 + (y – 4)2 = 62 hay (x + 2)2 + (y – 4)2 = 36.

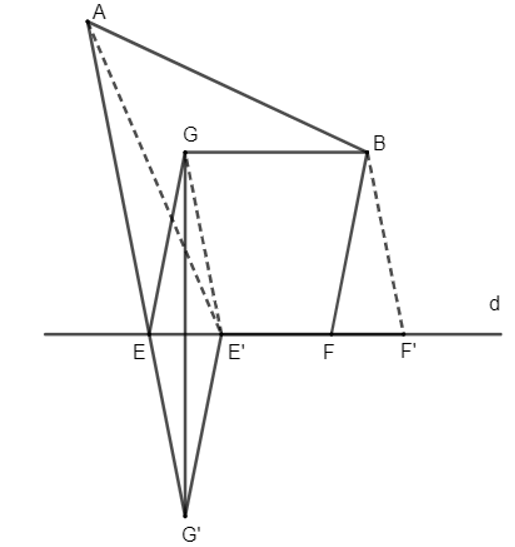
Bài 1.31 trang 33 Chuyên đề Toán 11: Cho đường thẳng d và hai điểm A, B cùng thuộc một nửa mặt phẳng bờ d. Hai điểm E, F thay đổi trên d sao cho $\overrightarrow{EF}$ không đổi. Xác định vị trí của hai điểm E, F để AE + BF nhỏ nhất.

Lời giải:

Ta có: $\left|\overrightarrow{EF}\right|=m$ (m > 0) không đổi.

Đặt $\overrightarrow{u}=\overrightarrow{EF }\left(\overrightarrow{u}\ne \overrightarrow{0}\right)$, $\overrightarrow{u}$ không đổi, khi đó $\left|\overrightarrow{u}\right|=m$ không đổi.

Gọi G là ảnh của điểm B qua phép tịnh tiến theo vectơ $\overrightarrow{\mathrm{-u}}$. Khi đó $\overrightarrow{BG}=-\overrightarrow{u}$. Vì B cố định và $\overrightarrow{u}$ không đổi nên G cố định. Gọi G' là ảnh của G qua phép đối xứng trục d thì G' cố định.

Gọi giao điểm của AG' và đường thẳng d là E, trên d lấy điểm F thỏa mãn EF = m và $\overrightarrow{EF}=\overrightarrow{u}=-\overrightarrow{BG}$ hay $\overrightarrow{EF}=\overrightarrow{GB}$. Khi đó BGEF là hình bình hành nên BF = GE.

Mà G và G' đối xứng nhau qua d nên GE = G'E. Do đó BF = GE = G'E.

Ta có: AE + BF = AE + G'E = AG' (1).

Ta có E và F như trên là hai điểm cần tìm để AE + BF nhỏ nhất.

Thật vậy, gọi E' và F' là 2 điểm trên d, khác E và F sao cho $\overrightarrow{E\text{'}F\text{'}}=\overrightarrow{u}$ và $\left|\overrightarrow{E\text{'}F\text{'}}\right|=\left|\overrightarrow{u}\right|=m$.

Ta có: AE' + BF' = AE' + GE' = AE' + G'E' > AG' (2) (bất đẳng thức trong tam giác AG'E').

Từ (1) và (2) suy ra AE + BF < AE' + BF'. Từ đó suy ra điều phải chứng minh.​​

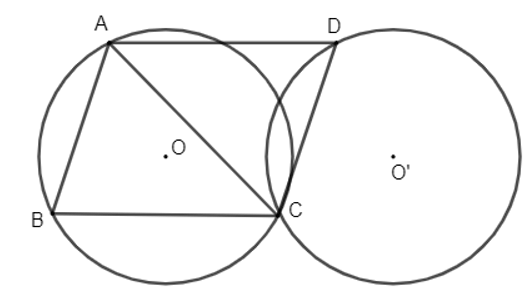
Bài 1.32 trang 33 Chuyên đề Toán 11: Cho tam giác ABC nội tiếp đường tròn tâm O. Các đỉnh B, C cố định còn đỉnh A thay đổi trên đường tròn đó. Vẽ hình bình hành ABCD. Chứng minh rằng điểm D luôn thuộc một đường tròn cố định.

Lời giải:

Vì ABCD là hình bình hành nên $\overrightarrow{AD}=\overrightarrow{BC}$.

Do B, C cố định nên vectơ $\overrightarrow{BC}$ cố định.

Khi đó ta có phép tịnh tiến theo vectơ $\overrightarrow{BC}$ biến điểm A thành điểm D. Mặt khác, A thuộc đường tròn tâm O ngoại tiếp tam giác ABC nên D thuộc đường tròn tâm O' cố định là ảnh của đường tròn tâm O qua phép tịnh tiến theo vectơ $\overrightarrow{BC}$. Ở đó, bán kính hai đường tròn bằng nhau và O' là ảnh của O qua phép tịnh tiến theo vectơ $\overrightarrow{BC}$ được xác định bởi $\overrightarrow{OO\text{'}}=\overrightarrow{BC}$.​

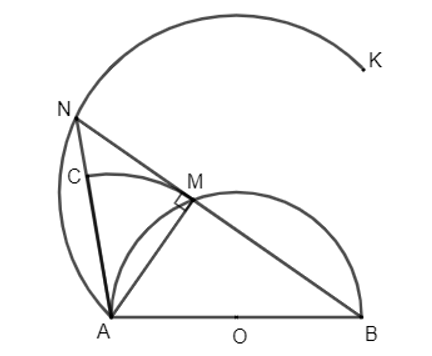
Bài 1.33 trang 33 Chuyên đề Toán 11: Cho nửa đường tròn tâm O, đường kính AB và điểm M trên nửa đường tròn đó. Dựng về phía ngoài của tam giác ABM tam giác AMN vuông cân tại M. Chứng minh rằng khi M thay đổi trên nửa đường tròn thì điểm N luôn thuộc một nửa đường tròn cố định.

Lời giải:

Trên cạnh AN, lấy điểm C sao cho AC = AM.

Tam giác AMN vuông cân tại M nên $\widehat{CAM}=\widehat{NAM}=45°$ và AN = $\sqrt{2}$AM = $\sqrt{2}$AC.

Vì AM = AC và $\widehat{CAM}=45°$ nên ta có phép quay tâm A, góc quay 45° biến điểm M thành điểm C.

Vì AN = $\sqrt{2}$AC và C thuộc AN nên $\sqrt{2}$, do đó ta có phép vị tự tâm A, tỉ số $\sqrt{2}$ biến điểm C thành điểm N.

Như vậy, phép đồng dạng có được bằng cách thực hiện liên tiếp phép quay tâm A, góc quay 45° và phép vị tự tâm A, tỉ số $\sqrt{2}$ biến điểm M thành điểm N. Mặt khác, M thuộc nửa đường tròn đường kính AB nên N thuộc nửa đường tròn đường kính AK cố định là ảnh của nửa đường tròn đường kính AB qua phép đồng dạng có được bằng cách thực hiện liên tiếp phép quay tâm A, góc quay 45° và phép vị tự tâm A, tỉ số $\sqrt{2}$. Ở đó K là ảnh của B qua phép đồng dạng trên, K thỏa mãn $\widehat{BAK}=45°$ (theo chiều dương) và AK = $\sqrt{2}$AB. ​

Bài 1.34 trang 33 Chuyên đề Toán 11: Bằng quan sát và đo đạc, hãy cho biết hai hình sau (H.1.55) có đồng dạng với nhau hay không.

Lời giải:

Thực hiện đo đạc và quan sát, ta nhận thấy hai hình đã cho không đồng dạng với nhau.​