Giải chuyên đề Toán 11 (Kết nối tri thức) Bài 3: Phép đối xứng trục

Giải Chuyên đề Toán 11 Bài 3: Phép đối xứng trục

1. Phép đối xứng trục

HĐ1 trang 12 Chuyên đề Toán 11: Cầu Ponte Sisto in hình dưới dòng sông Tiber, tạo nên một hình ảnh có tính đối xứng trục.

a) Hãy chỉ ra trục đối xứng của hình ảnh đó.

b) Có thể đếm được bao nhiêu hình bóng điện dưới sông? Mỗi hình đó là ảnh dưới sông của bóng điện nào trên cầu?

Lời giải:

a) Đường thẳng giao bởi cầu và mặt nước trên dòng sông là trục đối xứng của hình ảnh đó (đường màu xanh trong hình vẽ).

b) Có thể đếm được 5 bóng điện dưới dòng sông. Mỗi hình đó là ảnh dưới sông của bóng điện tương ứng với từng số thứ tự trên cầu như ảnh.

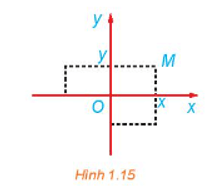
Luyện tập 1 trang 13 Chuyên đề Toán 11: Xét mặt phẳng tọa độ Oxy (H.1.15). Trong các khẳng định sau, chọn các khẳng định đúng.

a) Phép đối xứng trục Ox biến mỗi điểm M(x; y) thành điểm có tọa độ (x; – y).

b) Phép đối xứng trục Oy biến mỗi điểm M(x; y) thành điểm có tọa độ (– x; y).

c) Phép đối xứng trục Ox biến A(1; 2) thành điểm A'(– 1; – 2).

Lời giải:

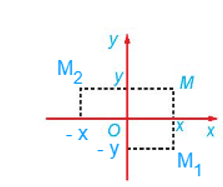
Từ hình vẽ ta thấy:

+) Phép đối xứng trục Ox biến mỗi điểm M(x; y) thành điểm M1(x; – y).

+) Phép đối xứng trục Oy biến mỗi điểm M(x; y) thành điểm M2(– x; y).

Do đó, phép đối xứng trục Ox biến điểm A(1; 2) thành A'(1; – 2).

Vậy các khẳng định a), b) đúng và khẳng định c) sai.​

2. Tính chất

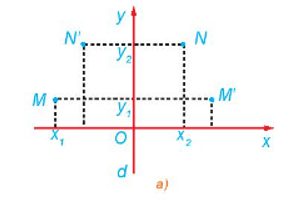
HĐ2 trang 14 Chuyên đề Toán 11: Cho phép đối xứng trục d biến M thành M', N thành N'. Xét hệ trục tọa độ Oxy sao cho trục Oy trùng với d (H.1.16a). Giả sử M có tọa độ là (x1; y1), N có tọa độ là (x2; y2).

a) Hãy cho biết tọa độ của M', N'.

b) Tính MN2, M'N'2 theo tọa độ của các điểm tương ứng.

c) So sánh độ dài các đoạn thẳng MN, M'N'.

Lời giải:

a) M' và N' lần lượt là ảnh của M và N qua phép đối xứng trục d (trục Oy).

Do đó M'(– x1; y1) và N'(– x2; y2).

b) Ta có: $M{N}^2={\left(\sqrt{{\left(x_2-x_1\right)}^2+{\left(y_2-y_1\right)}^2}\right)}^2$= (x2 – x1)2 + (y2 – y1)2

$M\text{'}N{\text{'}}^2={\left(\sqrt{{\left(-x_2-\left(-x_1\right)\right)}^2+{\left(y_2-y_1\right)}^2}\right)}^2$= (– x2 + x1)2 + (y2 – y1)2.

c) Ta có: (x2 – x1)2 = (x1 – x2)2 = (– x2 + x1)2.

Do đó (x2 – x1)2 + (y2 – y1)2 = (– x2 + x1)2 + (y2 – y1)2 hay MN2 = M'N'2.

Suy ra MN = M'N'.

Luyện tập 2 trang 14 Chuyên đề Toán 11: Trong mặt phẳng tọa độ Oxy, cho đường thẳng d: 3x – y – 1 = 0. Viết phương trình đường thẳng d' là ảnh của đường thẳng d qua phép đối xứng trục Ox.

Lời giải:

Cách 1:

Lấy hai điểm A(0; – 1) và B(1; 2) thuộc d.

Gọi A', B' lần lượt là ảnh của A, B qua phép đối xứng trục Ox.

Khi đó A'(0; 1) và B'(1; – 2).

Vì d' là ảnh của đường thẳng d qua phép đối xứng trục Ox nên A' và B' thuộc d'.

Ta có: $\overrightarrow{A\text{'}B\text{'}}=\left(1;-3\right)$. Suy ra $\overrightarrow{n_{d\text{'}}}=\left(3;1\right)$.

Vậy d' có phương trình là 3(x – 0) + (y – 1) = 0 hay 3x + y – 1 = 0.

Cách 2:

Gọi M'(x'; y') là ảnh của M(x; y) qua phép đối xứng trục Ox. Khi đó x' = x và y' = – y.

Ta có: M ∈ d ⇔ 3x – y – 1 = 0 ⇔ 3x' – (– y') – 1 = 0 ⇔ 3x' + y' – 1 = 0 ⇔ M' thuộc đường thẳng d' có phương trình là 3x + y – 1 = 0.

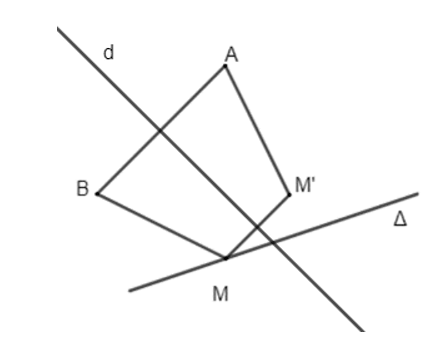
Luyện tập 3 trang 15 Chuyên đề Toán 11: Cho đường thẳng ∆ và hai điểm A, B, sao cho ∆ không phải là đường trung trực của đoạn thẳng AB. Điểm M thay đổi trên ∆ (M không thuộc đường thẳng AB). Gọi M' là điểm sao cho A, B, M, M' là 4 đỉnh của một hình thang cân nhận AB là một cạnh đáy. Chứng minh rằng M' thay đổi trên một đường thẳng cố định.

Lời giải:

Gọi d là đường trung trực của đoạn thẳng AB. Vì AB cố định nên d cố định.

Do A, B, M, M' là 4 đỉnh của hình thang cân nhận AB là một cạnh đáy nên MM' là đáy còn lại của hình thang cân và đường trung trực d của đoạn thẳng AB cũng là đường trung trực của đoạn thẳng MM'. Do đó M' là ảnh của điểm M qua phép đối xứng trục d.

Mặt khác, M thuộc đường thẳng ∆ nên M' thuộc đường thẳng ∆' là ảnh của đường thẳng ∆ qua phép đối xứng trục d.

Vậy rằng M' thay đổi trên một đường thẳng cố định ∆' là ảnh của đường thẳng ∆ qua phép đối xứng trục d.​

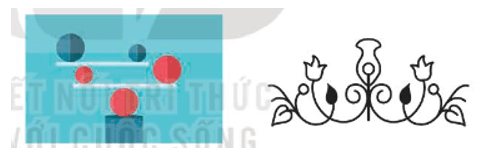
Vận dụng trang 15 Chuyên đề Toán 11: Bằng quan sát, hãy cho biết, trong hai hình ảnh bên, hình nào có trục đối xứng.

Lời giải:

Quan sát hình ảnh ta thấy hình thứ hai từ trái sang có trục đối xứng.

Bài tập

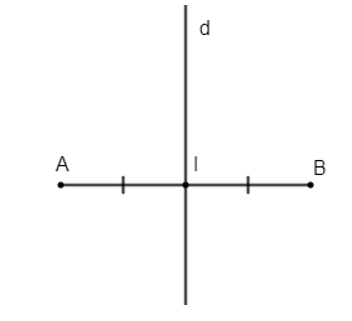
Bài 1.6 trang 15 Chuyên đề Toán 11: Cho hai điểm phân biệt A và B. Xác định phép đối xứng trục biến điểm A thành điểm B.

Lời giải:

Cách xác định:

- Nối điểm A với điểm B;

- Xác định trung điểm I của AB. Qua I vẽ đường thẳng d vuông góc với AB.

Khi đó d là đường trung trực của đoạn thẳng AB.

Vậy ta có phép đối xứng trục d biến điểm A thành điểm B.​

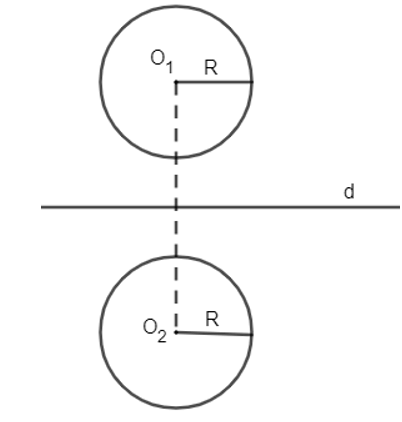
Bài 1.7 trang 15 Chuyên đề Toán 11: Cho hai đường tròn không đồng tâm, những có cùng bán kính (O1; R) và (O2; R). Xác định phép đối xứng trục biến (O1; R) thành (O2; R).

Lời giải:

Phép đối xứng trục biến đường tròn thành đường tròn có cùng bán kính và có tâm là ảnh của tâm nên ta xác định phép đối xứng trục biến đường tròn (O1; R) thành đường tròn (O2; R) thì chỉ cần xác định phép đối xứng trục biến tâm O1 thành tâm O2.

Ta xác định đường trung trực d của đoạn thẳng O1O­2. Khi đó phép đối xứng trục d biến O1 thành O2. Vậy phép đối xứng trục d biến đường tròn (O1; R) thành đường tròn (O2; R).​

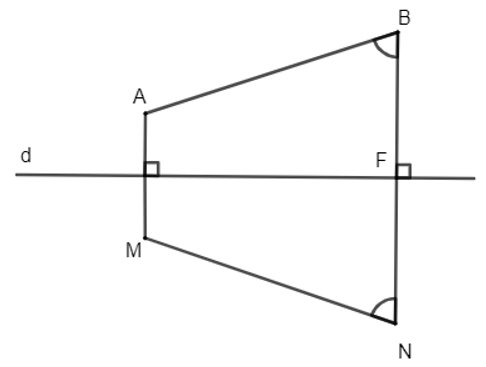
Bài 1.8 trang 15 Chuyên đề Toán 11: Cho đường thẳng d và hai điểm phân biệt A, B sao cho đường thẳng AB không vuông góc với d. Gọi M, N tương ứng là các điểm đối xứng với A, B qua d. Hỏi A, B, M, N có là 4 đỉnh của một hình thang cân hay không?

Lời giải:

Vì M, N tương ứng là các điểm đối xứng với A, B qua d nên phép đối xứng trục d biến điểm A thành điểm M và biến điểm B thành điểm N. Do đó, d là đường trung trực của đoạn thẳng AM và đoạn thẳng BN. Suy ra AM // BN (vì cùng vuông góc với d).

Suy ra tứ giác AMNB là hình thang (1).

Gọi F là trung điểm của BN, khi đó F thuộc đường trung trực d của đoạn thẳng BN nên phép đối xứng trục d biến điểm F thành chính nó.

Từ đó suy ra phép đối xứng trục d biến góc ABF thành góc MNF nên $\widehat{ABF}=\widehat{MNF}$ hay $\widehat{ABN}=\widehat{MNB}$ (2).

Từ (1) và (2) suy ra tứ giác AMNB là hình thang cân.

Vậy A, B, M, N là 4 đỉnh của một hình thang cân.​

Bài 1.9 trang 15 Chuyên đề Toán 11: Trong mặt phẳng tọa độ Oxy, cho ∆: x + 2y – 1 = 0. Viết phương trình đường thẳng d đối xứng với ∆ qua trục Ox.

Lời giải:

Đường thẳng d đối xứng với ∆ qua trục Ox hay d là ảnh của ∆ qua phép đối xứng trục Ox.

Cách 1:

Lấy hai điểm A(1; 0) và B(– 1; 1) thuộc ∆.

Gọi A', B' lần lượt là ảnh của A, B qua phép đối xứng trục Ox.

Khi đó A'(1; 0) và B'(– 1; – 1).

Vì d là ảnh của đường thẳng ∆ qua phép đối xứng trục Ox nên A' và B' thuộc d.

Ta có: $\overrightarrow{A\text{'}B\text{'}}=\left(-2;-1\right)$​. Suy ra $\overrightarrow{n_d}=\left(1;-2\right)$​.

Vậy d có phương trình là 1(x – 1) – 2(y – 0) = 0 hay x – 2y – 1 = 0.

Cách 2:

Gọi M'(x'; y') là ảnh của M(x; y) qua phép đối xứng trục Ox. Khi đó x' = x và y' = – y.

Ta có: M ∈ ∆ ⇔ x + 2y – 1 = 0 ⇔ x' + 2.(– y') – 1 = 0 ⇔ x' – 2y' – 1 = 0 ⇔ M' thuộc đường thẳng d có phương trình là x – 2y – 1 = 0.

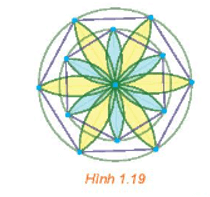
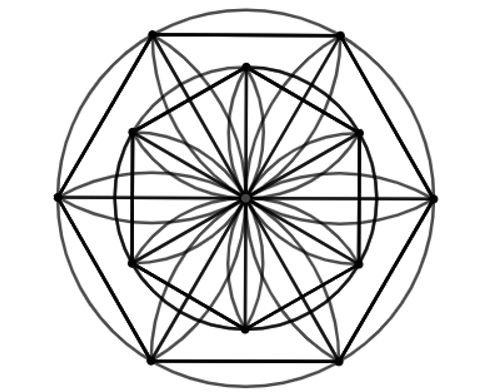
Bài 1.10 trang 15 Chuyên đề Toán 11: Dùng com-pa, thước kẻ, bút, hãy vẽ lại các nét thẳng và tròn trong Hình 1.19.

Lời giải:

Sử dụng tính đối xứng trục, ta vẽ được hình: