Câu hỏi:
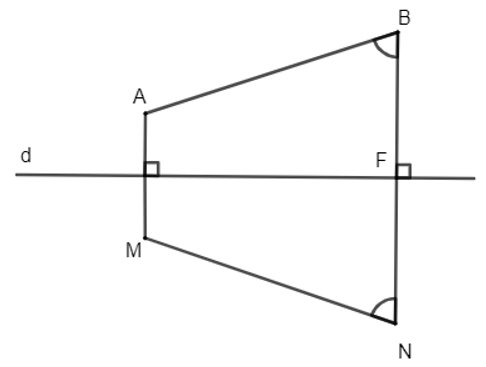
117 lượt xemBài 1.8 trang 15 Chuyên đề Toán 11: Cho đường thẳng d và hai điểm phân biệt A, B sao cho đường thẳng AB không vuông góc với d. Gọi M, N tương ứng là các điểm đối xứng với A, B qua d. Hỏi A, B, M, N có là 4 đỉnh của một hình thang cân hay không?
Lời giải
Hướng dẫn giải:
Vì M, N tương ứng là các điểm đối xứng với A, B qua d nên phép đối xứng trục d biến điểm A thành điểm M và biến điểm B thành điểm N. Do đó, d là đường trung trực của đoạn thẳng AM và đoạn thẳng BN. Suy ra AM // BN (vì cùng vuông góc với d).
Suy ra tứ giác AMNB là hình thang (1).
Gọi F là trung điểm của BN, khi đó F thuộc đường trung trực d của đoạn thẳng BN nên phép đối xứng trục d biến điểm F thành chính nó.
Từ đó suy ra phép đối xứng trục d biến góc ABF thành góc MNF nên hay (2).
Từ (1) và (2) suy ra tứ giác AMNB là hình thang cân.
Vậy A, B, M, N là 4 đỉnh của một hình thang cân.
ĐỀ THI LIÊN QUAN:
-
34 câu hỏi 89 lượt thi