Câu hỏi:
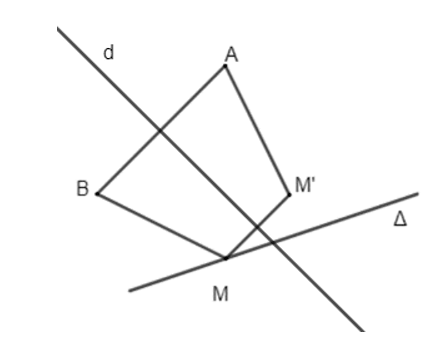
88 lượt xemLuyện tập 3 trang 15 Chuyên đề Toán 11: Cho đường thẳng ∆ và hai điểm A, B, sao cho ∆ không phải là đường trung trực của đoạn thẳng AB. Điểm M thay đổi trên ∆ (M không thuộc đường thẳng AB). Gọi M' là điểm sao cho A, B, M, M' là 4 đỉnh của một hình thang cân nhận AB là một cạnh đáy. Chứng minh rằng M' thay đổi trên một đường thẳng cố định.
Lời giải
Hướng dẫn giải:
Gọi d là đường trung trực của đoạn thẳng AB. Vì AB cố định nên d cố định.
Do A, B, M, M' là 4 đỉnh của hình thang cân nhận AB là một cạnh đáy nên MM' là đáy còn lại của hình thang cân và đường trung trực d của đoạn thẳng AB cũng là đường trung trực của đoạn thẳng MM'. Do đó M' là ảnh của điểm M qua phép đối xứng trục d.
Mặt khác, M thuộc đường thẳng ∆ nên M' thuộc đường thẳng ∆' là ảnh của đường thẳng ∆ qua phép đối xứng trục d.
Vậy rằng M' thay đổi trên một đường thẳng cố định ∆' là ảnh của đường thẳng ∆ qua phép đối xứng trục d.
ĐỀ THI LIÊN QUAN:
-
34 câu hỏi 89 lượt thi