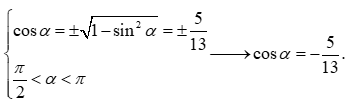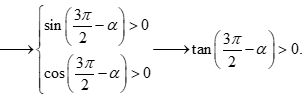50 câu Trắc nghiệm Giá trị lượng giác của góc lượng giác (có đáp án 2024) – Toán 11 Kết nối tri thức

Bộ 50 câu hỏi trắc nghiệm Toán 11 (có đáp án) Bài 1: Giá trị lượng giác của góc lượng giác đầy đủ các mức độ sách Kết nối tri thức giúp học sinh ôn luyện trắc nghiệm Toán 11 Bài 1.

1 208 lượt xem

Bài trước

Bài sau

Trắc nghiệm Toán 11 Bài 1: Giá trị lượng giác của góc lượng giác

Câu 1. Cho góc $α$ thỏa mãn sin $α$ + cos $α$ = $\frac{5}{4}$ . Tính P = sin $α$ .cos $α$ .

A. P = $\frac{9}{16}$ . B. P = $\frac{9}{32}$ . C. P = $\frac{9}{8}$ . D. P = $\frac{1}{8}$ .

Hướng dẫn giải

Đáp án đúng là: B

Từ giả thiết, ta có (sin $α$ +cos $α$ )2 = $\frac{25}{16} \Leftrightarrow$ 1 +2sin $α$ .cos $α$ = $\frac{25}{16}$

Câu 2. Tính giá trị biểu thức P = tan10o.tan20o.tan30o.....tan80o

A. P = 0 B. P = 1 C. P = 4 D. P = 8

Hướng dẫn giải

Đáp án đúng là: B

Áp dụng công thức tanx.tan(90o-x) = tanx.cotx = 1.

Do đó P = 1.

Câu 3. Cho P = sin( $π + α$ ).cos( $π - α$ ) và Q = $\sin (\frac{π}{2} - α) . \cos (\frac{π}{2} + α) .$ Mệnh đề nào dưới đây là đúng?

A. P+Q = 0 B. P+Q = -1 C. P+Q = 1 D. P+Q = 2

Hướng dẫn giải

Đáp án đúng là: A

Ta có P = sin( $π + α$ ).cos( $π - α$ ) = -sin $α$ .(-cos $α$ ) = sin $α$ .cos $α$ .

Và Q = $\sin (\frac{π}{2} - α) . \cos (\frac{π}{2} + α) .$ = cos $α$ .(-sin $α$ ) = -sin $α$ .cos $α$ .

Khi đó P+Q = sin $α$ .cos $α$ - sin $α$ .cos $α$ = 0

Câu 4. Cho góc $α$ thỏa mãn sin $α$ = $\frac{12}{13}$ và $\frac{π}{2} < α < π$ . Tính cos $α$ .

A. cos $α$ = $\frac{1}{13}$ . B. cos $α$ = $\frac{5}{13}$ . C. cos $α$ = - $\frac{5}{13}$ D. cos $α$ = - $\frac{1}{13}$ .

Hướng dẫn giải

Đáp án đúng là: D

Ta có 12 Bài tập Giá trị lượng giác của góc lượng giác (có đáp án) | Kết nối tri thức Trắc nghiệm Toán 11

Câu 5. Cho góc $α$ thỏa mãn cot $α$ = $\frac{1}{3}$ . Tính $P = \frac{3 \sin α + 4 \cos α}{2 \sin α - 5 \cos α} .$

A. P = - $\frac{15}{13}$ B. P = $\frac{15}{13}$ . C. P = -13 D. P = 13.

Hướng dẫn giải

Đáp án đúng là: D

Chia cả tử và mẫu của P cho sin $α$ ta được $P = \frac{3 + 4 \cot α}{2 - 5 \cot α} = \frac{3 + 4. \frac{1}{3}}{2 - 5. \frac{1}{3}} = 13$ .

Câu 6. Biết A, B, C là các góc của tam giác ABC, mệnh đề nào sau đây đúng:

A. sin(A+C) = -sinB B. cos(A+C) = -cosB.

C. tan(A+C) = tanB D. cot(A+C) = cotB.

Hướng dẫn giải

Đáp án đúng là: B

Vì A, B, C là ba góc của một tam giác suy ra A+C = $π$ -B.

Khi đó (A+C) = sin( $π$ -B) = sinB; cos(A+C) = cos( $π$ -B) = -cosB.

tan(A+C) = tan( $π$ -B) = -tanB; cot(A+C) = cot( $π$ -B) = -cotB.

Câu 7. Khẳng định nào sau đây là đúng khi nói về “đường tròn lượng giác”?

A. Mỗi đường tròn là một đường tròn lượng giác.

B. Mỗi đường tròn có bán kính R = 1 là một đường tròn lượng giác.

C. Mỗi đường tròn có bán kính R = 1, tâm trùng với gốc tọa độ là một đường tròn lượng giác.

D. Mỗi đường tròn định hướng có bán kính R = 1, tâm trùng với gốc tọa độ là một đường tròn lượng giác.

Hướng dẫn giải

Đáp án đúng là: D

Câu 8. Đổi số đo của góc 70o sang đơn vị radian.

A. $\frac{70}{π} .$ B. $\frac{7}{18} .$ C. $\frac{7 π}{18} .$ D. $\frac{7}{18 π} .$

Hướng dẫn giải

Đáp án đúng là:C

Áp dụng công thức $α = \frac{a . π}{180}$ với $α$ tính bằng radian, a tính bằng độ.

Ta có $α = \frac{a . π}{180} = \frac{70 π}{180} = \frac{7 π}{18}$ .

Câu 9. Tính độ dài l của cung trên đường tròn có bán kính bằng 20cm và số đo $\frac{π}{16} .$

A. l = 3,93cm. B. l = 2,94cm. C. l = 3,39cm D. l = 1,49cm

Hướng dẫn giải

Đáp án đúng là:A

Áp dụng công thức $l = R α = 20. \frac{π}{16} \approx 3, 93 cm.$

Câu 10. Với mọi số thực $α$ , ta có $\sin (\frac{9 π}{2} + α)$ bằng

A. -sin $α$ B. cos $α$ C. sin $α$ D. -cos $α$

Hướng dẫn giải

Đáp án đúng là: B

Ta có $\sin (\frac{9 π}{2} + α) = \sin (4 π + \frac{π}{2} + α) = \sin (\frac{π}{2} + α) = \cos α .$

Câu 11. Cho $π < α < \frac{3 π}{2} .$ Khẳng định nào sau đây đúng?

A. tan $(\frac{3 π}{2} - α)$ <0. B. tan $(\frac{3 π}{2} - α)$ >0

C. tan $(\frac{3 π}{2} - α)$ $\leq$ 0 D. tan $(\frac{3 π}{2} - α)$ $\geq$ 0

Hướng dẫn giải

Đáp án đúng là: B

Ta có $π < α < \frac{3 π}{2} \to 0 < \frac{3 π}{2} - α < \frac{π}{2}$ 12 Bài tập Giá trị lượng giác của góc lượng giác (có đáp án) | Kết nối tri thức Trắc nghiệm Toán 11

Câu 12. Cho góc $α$ thỏa mãn $π < α < \frac{3 π}{2}$ và sin $α$ -2cos $α$ = 1. Tính P = 2tan $α$ - cot $α$ .

A. P = $\frac{1}{2}$ . B. P = $\frac{1}{4}$ . C. P = $\frac{1}{6}$ . D. P = $\frac{1}{8}$ .

Hướng dẫn giải

Đáp án đúng là: C

Với $π < α < \frac{3 π}{2}$ s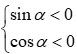uy ra 12 Bài tập Giá trị lượng giác của góc lượng giác (có đáp án) | Kết nối tri thức Trắc nghiệm Toán 11 .

Ta có 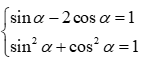12 Bài tập Giá trị lượng giác của góc lượng giác (có đáp án) | Kết nối tri thức Trắc nghiệm Toán 11 $\Rightarrow {(1 + 2 \cos α)}^{2} + \cos^{2} α = 1$

$\Leftrightarrow 5 \cos^{2} α + 4 \cos α = 0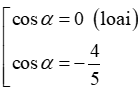 \Leftrightarrow$ 12 Bài tập Giá trị lượng giác của góc lượng giác (có đáp án) | Kết nối tri thức Trắc nghiệm Toán 11 .

Từ hệ thức $\sin^{2} α + \cos^{2} α = 1$ , suy ra $\sin α = - \frac{3}{5}$ (do sin $α$ <0) $\to$ tan $α$ = $\frac{\sin α}{\cos α} = \frac{3}{4}$ và $\cot α = \frac{\cos α}{\sin α} = \frac{4}{3} .$

Thay $\tan α = \frac{3}{4}$ và $\cot α = \frac{4}{3}$ vào P, ta được P = $\frac{1}{6}$ .

1 208 lượt xem

Bài trước

Bài sau

50 câu Trắc nghiệm Giá trị lượng giác của góc lượng giác (có đáp án 2024) – Toán 11 Kết nối tri thức

Giới thiệu

Liên kết

Chính sách

Kết nối

50 câu Trắc nghiệm Giá trị lượng giác của góc lượng giác (có đáp án 2024) – Toán 11 Kết nối tri thức

CHỌN BỘ SÁCH BẠN MUỐN XEM