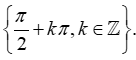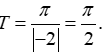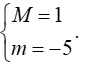50 câu Trắc nghiệm Hàm số lượng giác (có đáp án 2024) – Toán 11 Kết nối tri thức
Bộ 50 câu hỏi trắc nghiệm Toán 11 (có đáp án) Bài 3: Hàm số lượng giác đầy đủ các mức độ sách Kết nối tri thức giúp học sinh ôn luyện trắc nghiệm Toán 11 Bài 3.
Trắc nghiệm Toán 11 Bài 3: Hàm số lượng giác
Câu 1. Tìm chu kì T của hàm số y = cos3x + cos5x.
A. T = π B. T = 3π C. T = 2π D. T = 5π
Đáp án đúng là: C
Hàm số y = cos3x tuần hoàn với chu kì T1=2π3.
Hàm số Y = cos5x tuần hoàn với chu kì T2=2π5.
Suy ra hàm số y = cos3x + cos5x tuần hoàn với chu kì T = 2π
Câu 2. Tìm tập giá trị của hàm số y = 3cos2x + 5
A. T = [-1;1]. B. T = [-1;11] C. T = [2;8] D. T = [5;8]
Đáp án đúng là: C
Ta có -1≤cos2x≤1 → -3≤3cos2x≤3 → 2≤3cos2x+5≤8
→ 2≤y≤8→ T = [2;8].
Câu 3. Hàm số y = 5+4sin2xcos2x có tất cả bao nhiêu giá trị nguyên?
A. 3. B. 4. C. 5. D. 6.
Đáp án đúng là: C
Ta có y = 5+4sin2xcos2x = 5+2sin4x. .
Mà -1≤sin4x≤1 →-2≤2sin4x≤2 → 3≤5+2sin4x≤7
→ y≤7 →3≤y≤7y∈ℤ→y∈{3;4;5;6;7} nên y có 5 giá trị nguyên.
Câu 4. Tìm tập xác định D của hàm số y=2021sinx.
A. D = ℝ B. D = ℝ\{0}
C. D =ℝ\{kπ,∈ℤ} D. D = ℝ\
Đáp án đúng là: C
Hàm số xác định khi và chỉ khi sinx≠0 ⇔x≠kπ, k∈ℤ.
Vật tập xác định D = ℝ\{kπ,k∈ℤ}.
Câu 5. Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = sinx + cosx. Tính P = M - m.
A. P = 4 B. P = 2√2 C. P = √2 D. P = 2
Đáp án đúng là: B
Ta có y = sinx + cosx = √2sin(x+π4).
Mà -1≤sin(x+π4)≤1 →-√2≤√2sin(x+π4)≤√2
→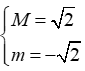
Câu 6. Tìm chu kì T của hàm số y = cos2x + sinπ2
A. T = 4π B. T = π C. T = 2π D. T = π2
Đáp án đúng là: A
Hàm số y = cos2x tuần hoàn với chu kì T1=2π2=π.
Hàm số y = sinx2 tuần hoàn với chu kì T2=2π12=4π.
Suy ra hàm số y = cos2x + sinx2 tuần hoàn với chu kì T = 4π.
Nhận xét. T là của T1 và T2
Câu 7. Hàm số nào sau đây có chu kì khác π?
A. y=sin(π3−2x). B. y=cos2(x+π4).
C. y = tan(-2x+1). D. y = cosxsinx
Đáp án đúng là: C
Vì y = tan(-2x+1) có chu kì
Nhận xét. Hàm số y = cosxsinx = 12sin2x có chu kỳ là π.
Câu 8. Trong các hàm số sau, hàm số nào có đồ thị đối xứng qua gốc tọa độ?
A. y=1sin3x. B. y=sin(x+π4).
C. y=√2cos(x−π4). D. y=√sin2x.
Đáp án đúng là: A
Viết lại đáp án B là y=sin(x+π4)=1√2(sinx+cosx).
Viết lại đáp án C là y=√2cos(x−π4)=sinx+cosx.
Kiểm tra được đáp án A là hàm số lẻ nên có đồ thị đối xứng qua gốc tọa độ.
Ta kiểm tra được đáp án B và C là các hàm số không chẵn, không lẻ.
Xét đáp án D:
- Hàm số xác định ⇔sin2x ≥0 ⇔ 2x∈[k2π;π+k2π] ⇔ x∈
-> D = 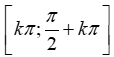
- Chọn x=π4∈D nhưng −x=−π4∉D. Vậy y=√sin2x không chẵn, không lẻ.
Câu 9. Trong các hàm số sau đây, hàm số nào không tuần hoàn?
A. y = cosx B. y = cos2x C. y = x2cosx. D. y = 1sin2x
Đáp án đúng là: C
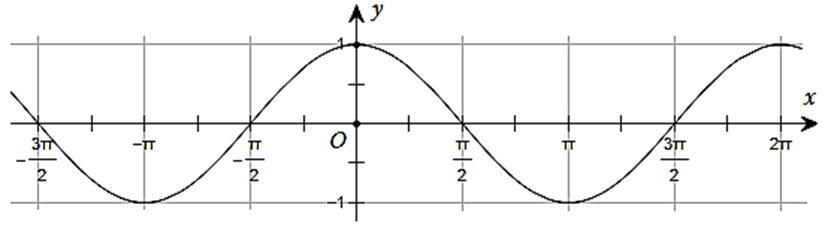
Câu 10. Đường cong trong hình dưới đây là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D.
Hỏi hàm số đó là hàm số nào?
A. y = 1+sin2x B. y = cosx C. y = -sinx D. y = -cosx
Đáp án đúng là: B
Ta thấy tại x = 0 thì y = 1. Do đó loại đáp án C và D.
Tại x = π2 thì y = 0. Do đó chỉ có đáp án B thỏa mãn.
Câu 11. Tìm giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số y = 3sinx - 2
A. M = 1, m = -5. B. M = 3, m = 1 C. M = 2, m = -2 D. M = 0, m = -2.
Đáp án đúng là: A
Ta có −1≤sinx≤1→−3≤3sinx≤3→−5≤3sinx−2≤1
→−5≤y≤1→
Câu 12. Trong các hàm số sau, hàm số nào là hàm số chẵn?
A. y = sin2x B. y = xcosx C. y = cosx.cotx D. y = tanxsinx
- Xét hàm số y = f(x) = sin2x.
TXĐ: D = ℝ. Do đó ∀x∈D⇒−x∈D.
Ta có f(-x) = sin(-2x) = -sin2x = -f(x) →f(x) là hàm số lẻ.
-Xét hàm số y = f(x) = xcosx.
TXĐ: D = ℝ. Do đó ∀x∈D⇒−x∈D.
Ta có f-x) = (-x).cos(-x) = -xcosx = -f(x) → f(x) là hàm số lẻ.
-Xét hàm số y = f(x) = cosx.cotx.
TXĐ: D = ℝ\{kπ(k∈ℤ)}. Do đó ∀x∈D⇒−x∈D.
Ta có f(-x) = cos(-x).cot(-x) = -cosxcotx = -f(x)→f(x) là hàm số lẻ.
- D = ℝ.Xét hàm số y = f(x) = tanxsinx.
TXĐ: D = ℝ\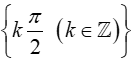
Ta có f(−x)=tan(−x)sin(−x)=−tanx−sinx=tanxsinx=f(x) →f(x) là hàm số chẵn.