Tập xác định của hàm số $y=\sqrt{\frac{1-\cos x}{1+\sin x}}$  là:

A. ℝ.

B. ∅.

Tập xác định của hàm số $y=\sqrt{1+\cos 2x}$  là:

A. ∅.

B. ℝ.

C. [– 1; + ∞).

D. 

Quan sát hai bức tranh em bé ôm chú gà ở phần mở đầu bài học và chỉ ra phép vị tự biến bức tranh nhỏ thành bức tranh lớn và phép vị tự biến bức tranh lớn thành bức tranh nhỏ.

Chứng minh rằng, phép vị tự V_{(O, 1)} là phép đồng nhất, phép vị tự V_{(o, – 1)} là phép đối xứng tâm O.

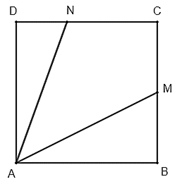
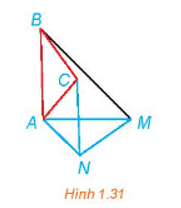
Trên một mảnh đất hình vuông ABCD, bác An đặt một chiếc đèn pin tại vị trí A chiếu chùm sáng phân kì sang phía góc C. Bác An nhận thấy góc chiếu sáng của đèn pin giới hạn bởi hai tia AM và AN, ở đó các điểm M, N lần lượt thuộc các cạnh BC, CD sao cho BM = $\frac{1}{2}$BC, DN = $\frac{1}{3}$DC (Hình 4).

a) Tính $\tan \left(\widehat{BAM}+\widehat{DAN}\right)$ .

b) Góc chiếu sáng của đèn pin bằng bao nhiêu độ?

Hình 4

Cho tam giác ABC, chứng minh rằng:

a) tan A + tan B + tan C = tan A . tan B . tan C (với điều kiện tam giác ABC không vuông);

b) $\tan \frac{A}{2}.\tan \frac{B}{2}+\tan \frac{B}{2}.\tan \frac{C}{2}+\tan \frac{C}{2}.\tan \frac{A}{2}=1$ .

Cho cos(a + 2b) = 2cos a. Chứng minh rằng: tan(a + b) tan b = $\frac{-1}{3}$ .  

Cho cos a = 0,2 với π < a < 2π. Tính $\sin \frac{a}{2}$ , $\cos \frac{a}{2}$ , $\tan \frac{a}{2}$ .

Cho $\sin a=\frac{2}{3}$  với $\frac{\pi }{2}<a<\pi$ . Tính:

a) cos a, tan a;

b) $\sin \left(a+\frac{\pi }{4}\right),\cos \left(a-\frac{5\pi }{6}\right),\tan \left(a+\frac{2\pi }{3}\right)$ ;

c) sin 2a, cos 2a.

Phép vị tự V_{(O, k)­} biến điểm O thành điểm nào? Nếu phép vị tự V_{(O, k)} biến điểm M thành điểm M' thì phép vị tự $V_{\left(O,\frac{1}{k}\right)}$ biến điểm M' thành điểm nào?

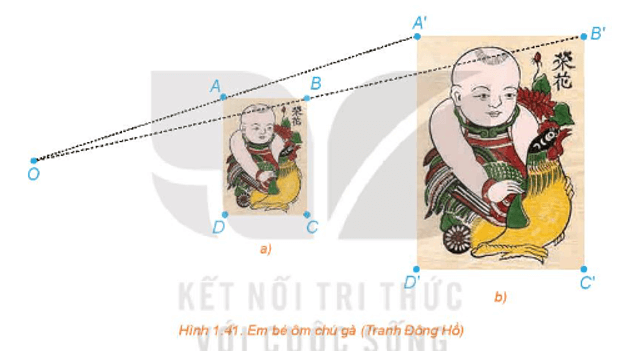
Trong hai bức tranh ở Hình 1.41, các hình chữ nhật ABCD, A'B'C'D' có các cạnh tương ứng song song, bức tranh lớn có kích thước gấp đôi bức tranh nhỏ.

a) Giải thích vì sao các đường thẳng AA', BB', CC', DD' cùng đi qua một điểm O.

b) Hãy tính các tỉ số $\frac{OA}{OA\text{'}},\frac{OB}{OB\text{'}},\frac{OC}{OC\text{'}},\frac{OD}{OD\text{'}}$.

c) Dùng thước thẳng nối hai điểm tương ứng nào đó trên hai bức tranh (chẳng hạn, đầu mỏ trên của chú gà ở hai bức tranh). Đường thẳng đó có đi qua O hay không?

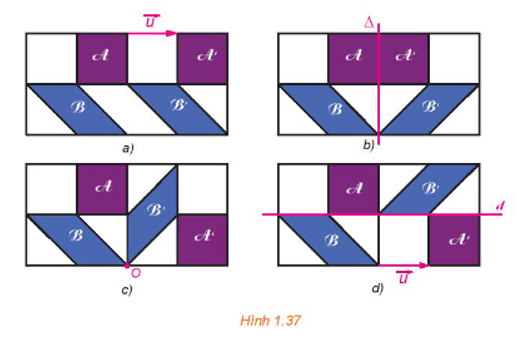
Hình 1.38 được vẽ dựa theo bức tranh Kị binh (horsmen) của Escher, gồm các hình bằng nhau mô tả các kị binh trên ngựa.

Bằng quan sát, hãy chỉ ra những khẳng định đúng trong các khẳng định sau:

a) Có phép tịnh tiến biến mỗi chiến binh thành một chiến binh cùng màu.

b) Có phép đối xứng trục biến mỗi chiến binh thành một chiến binh khác màu.

c) Có phép dời hình có được bằng cách thực hiện liên tiếp một phép đối xứng trục và một phép tịnh tiến biến mỗi kị binh thành một kị binh khác màu.

Cho một mảnh giấy hình thang cân ABCD (AB // CD). Hãy chỉ ra một cách cắt mảnh giấy đó thành hai mảnh giấy bằng nhau.

Bằng quuan sát, hãy chỉ ra trong mỗi hình trong Hình 1.37 một phép dời hình biến hình vuông ? thành hình vuông ?', đồng thời biến hình bình hành ℬ thành hình bình hành ℬ'.

Trong mặt phẳng tọa độ Oxy, cho vectơ $\overrightarrow{u}=\left(0;1\right)$. Những khẳng định nào trong các khẳng định sau là đúng?

a) Phép đối xứng trục Oy biến mỗi điểm M(x; y) thành điểm M'(– x; y).

b) Phép tịnh tiến theo vectơ $\overrightarrow{u}$ biến điểm M'(– x; y) thành điểm M''(– x; y + 1).

c) Thực hiện liên tiếp hai phép dời hình Đ_Oy­ và $T_{\overrightarrow{u}}$ (Đ_Oy trước, $T_{\overrightarrow{u}}$ sau) ta được phép dời hình biến mỗi điểm M(x; y) thành điểm M''(– x; y + 1).

d) Phép dời hình có được bằng cách thực hiện liên tiếp hai phép dời hình Đ_Oy và $T_{\overrightarrow{u}}$ biến điểm A(1; 2) thành điểm A''(– 1; 1).

Trong tình huống mở đầu, bằng quan sát (H.1.33), hãy chỉ ra phép dời hình:

a) Biến Hình a) thành Hình b).

b) Biến Hình b) thành Hình c).

c) Biến Hình a) thành Hình c).

d) Biến Hình c) thành Hình a).

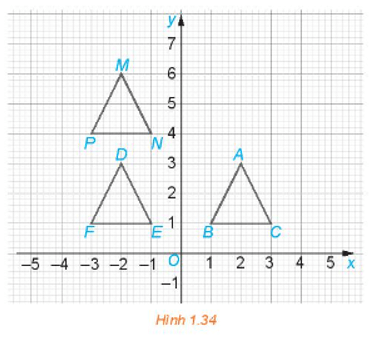
Trong mặt phẳng tọa độ Oxy ở Hình 1.34, gọi f là phép biến hình biến mỗi điểm có tọa độ (x; y) thành điểm có tọa độ (– x; y + 3). Trong các khẳng định sau, những khẳng định nào đúng.

a) f biến ∆ABC thành ∆DEF.

b) f biến ∆DEF thành ∆MNP.

c) f biến ∆ABC thành ∆MNP.

Các phép tịnh tiến, phép đối xứng trục, phép quay cùng có tính chất nào trong các tính chất sau?

a) Biến một vectơ thành vectơ bằng nó.

b) Biến một đường tròn thành một đường tròn cùng tâm.

c) Biến một đoạn thẳng thành đoạn thẳng bằng nó.

d) Biến một đường thẳng thành đường thẳng song song với nó.

Bằng quan sát, ta có cảm nhận rằng ba hình a), b), c) bằng nhau. Nếu cắt giấy, lấy riêng ra từng hình, thì ta có thể xếp chồng khít hai hình b) và c) với nhau, hãy úp khít hai hình a) và b) (cũng như hai hình a) và c)) vào nhau. Đối tượng toán học nào cho phép ta diễn đạt hai hình bằng nhau? Ta hãy cùng tìm hiểu trong bài học này.

Rút gọn biểu thức $A=\frac{\sin x+\sin 2x+\sin 3x}{\cos x+\cos 2x+\cos 3x}$  ta được kết quả là:

A. tan x. 

B. tan 3x.

C. tan 2x.

D. tan x + tan 2x + tan 3x.

Giá trị của biểu thức $P=\frac{\sin \frac{\pi }{9}+\sin \frac{5\pi }{9}}{\cos \frac{\pi }{9}+\cos \frac{5\pi }{9}}$  bằng:

A. $\frac{1}{\sqrt{3}}$ .

B. $-\frac{1}{\sqrt{3}}$ .

C. $\sqrt{3}$ .

D. $-\sqrt{3}$ .                                             

Nếu $\cos a=\frac{1}{3},\sin b=\frac{-2}{3}$  thì giá trị cos(a + b) cos(a − b) bằng:

A. $-\frac{2}{3}$ .

B. $\frac{1}{3}$ .

C. $\frac{2}{3}$ .

D. $-\frac{1}{3}$ .

Nếu $\cos a=\frac{\sqrt{5}}{3}$  thì giá trị của biểu thức $A=4\sin \left(a+\frac{\pi }{3}\right)\sin \left(a-\frac{\pi }{3}\right)$  bằng:

A. $-\frac{11}{9}$ .

B. $\frac{11}{9}$ .

C. $-\frac{1}{9}$ .

D. $\frac{1}{9}$ .

Nếu $\cos a=\frac{3}{4}$  thì giá trị của $\cos \frac{a}{2}\cos \frac{a}{2}$  bằng:

A. $\frac{23}{16}$ .

B. $\frac{7}{8}$ .

C. $\frac{7}{16}$ .

D. $\frac{23}{8}$ .

Rút gọn biểu thức cos(120° – x) + cos(120° + x) – cos x ta được kết quả là:

A. – 2cos x.

B. – cos x.

C. 0.

D. sin x – cos x.

Chọn đẳng thức đúng trong các đẳng thức sau:

A. ${\sin }^{4}x+{\cos }^{4}x=\frac{3-\cos 4x}{4}$ .

B. ${\sin }^{4}x+{\cos }^{4}x=\frac{3+\cos 4x}{4}$ .

C. ${\sin }^{4}x+{\cos }^{4}x=\frac{3+\cos 4x}{2}$ .

D. ${\sin }^{4}x+{\cos }^{4}x=\frac{3-\cos 4x}{2}$ .

Nếu $\sin \alpha =\frac{2}{3}$  thì giá trị của biểu thức $P=\left(1-3\cos 2\alpha \right)\left(2+3\cos 2\alpha \right)$  bằng:

A. $\frac{11}{9}$ .

B. $\frac{12}{9}$ .

C. $\frac{13}{9}$ .

D. $\frac{14}{9}$ .

Nếu $\sin \alpha =\frac{1}{\sqrt{3}}$  với $0<\alpha <\frac{\pi }{2}$  thì giá trị của $\cos \left(\alpha +\frac{\pi }{3}\right)$  bằng:

A. $\frac{\sqrt{6}}{6}-\frac{1}{2}$ .

B. $\sqrt{6}-3$ .

C. $\frac{\sqrt{6}}{6}-3$ .

D. $\sqrt{6}-\frac{1}{2}$.

Cho hai góc a và b với tan a = $\frac{1}{7}$  và tanb = $\frac{3}{4}.$  Khi đó, tan(a + b) bằng:

A. 1.

B. $-\frac{17}{31}$ .

C. $\frac{17}{31}$ .

D. – 1.

Bằng quan sát Hình 1.32, hãy chỉ ra một cách cắt hình đó thành ba phần giống nhau.

Trong mặt phẳng tọa độ Oxy, cho đường tròn (C): (x – 2)² + y² = 1.

a) Tìm tọa độ tâm đường tròn (C') là ảnh của đường tròn (C) qua $Q_{\left(O,\frac{\pi }{2}\right)}$

b) Viết phương trình (C').

Cho hình bình hành ABCD với tâm O.

a) Tìm ảnh của đường thẳng AB qua phép đối xứng tâm O.

b) Tìm ảnh của tam giác ABC qua phép đối xứng tâm O.

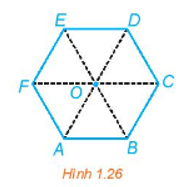
Cho hình vuông ABCD có tâm O. Trên đường tròn ngoại tiếp hình vuông, theo chiều dương (ngược chiều kim đồng hồ), thứ tự các đỉnh hình vuông là A, B, C, D.

a) Tìm ảnh của các điểm A, B, C, D qua phép quay tâm O góc quay $\frac{\pi }{2}$.

b) Mỗi phép quay Q_{(O, o)}, $Q_{\left(O,\frac{\pi }{2}\right)},Q_{\left(O,\pi \right)},Q_{\left(O,\frac{3\pi }{2}\right)}$ biến hình vuông ABCD thành hình nào?

Trong Hình 1.31, BAM và CAN là các tam giác vuông cân tại A. Hãy chỉ ra một phép quay biến tam giác ABC thành tam giác AMN.

Trong tình huống mở đầu, mặt bàn tròn đặt đồ ăn được thiết kế để có thể quay quanh tâm mặt bàn. Coi mặt bàn tròn là hình tròn tâm O, bán kính R. Hỏi, khi thuwjc hiện phép quay tâm O với góc quay α bất kì thì:

- Điểm O biến thành điểm nào?

- Đường tròn (O, R) biến thành đường tròn nào?

- Vị trí của mặt bàn có bị dịch chuyển hay không?

Trong Hình 1.26, ABCDEF là lục giác đều có tâm O. Tìm ảnh của tam giác ACE qua các phép quay $Q_{\left(O,\frac{\pi }{3}\right)},Q_{\left(O,-\frac{2\pi }{3}\right)}$.

Khi mặt bàn ăn quay, mặc dù các đĩa thức ăn trên bàn đều dịch chuyển tới vị trí mới nhưng khoảng cách giữa hai đĩa thức ăn có bị thay đổi hay không?

Trong Hình 1.22, tam giác ABC đều.

Gọi D là ảnh của C qua phép quay Q_{(A, 60°)}.

Hỏi B và D có mối quan hệ gì đối với đường thẳng AC?

Phép quay với góc quay bằng 0 có gì đặc biệt?

Ở mặt bàn ăn quay nói trên, trong một lần quay, nếu một đĩa thức ăn trên bàn được quay một phần tư vòng tới vị trí người mới, thì mỗi đĩa không đặt ở chính giữa bàn có được quay một phần tư vòng tới vị trí mới hay không?