Một xí nghiệp dự định chia đều 12 600 000 đồng để thưởng cho các công nhân tham gia hội thao nhân ngày thành lập xí nghiệp. Khi đến ngày hội thao chỉ có 80% số công nhân tham gia, vì thế mỗi người tham gia hội thao được nhận thêm 105 000 đồng. Tính số công nhân dự định tham gia lúc đầu.

Một người đi xe đạp từ A đến B cách nhau 60km. Sau 1 giờ 40 phút, trên cùng quãng đường đó, một xe máy cũng đi từ A đến B và đến B sớm hơn xe đạp 1 giờ. Tính tốc độ của mỗi xe, biết rằng tốc độ của xe máy gấp 3 lần tốc độ của xe đạp.

Giải các phương trình:

a) $\frac{x+5}{x-3}+2=\frac{2}{x-3}$;

b) $\frac{3x+5}{x+1}+\frac{2}{x}=3$;

c) $\frac{x+3}{x-2}+\frac{x+2}{x-3}=2$;

d) $\frac{x+2}{x-2}-\frac{x-2}{x+2}=\frac{16}{x^2-4}$.

Giải các phương trình:

a) $3x(x-4)+7(x-4)=0$;

b) $5x(x+6)-2x-12=0$;

c) $x^2-x-(5x-5)=0$;

d) $(3x-2{)}^2-(x+6{)}^2=0$.

Giải các phương trình:

a) $5x(2x-3)=0$;

b) $(2x-5)(3x+6)=0$;

c) $\left(\frac{2}{3}x-1\right)\left(\frac{1}{2}x+3\right)=0$;

d) $(2,5t-7,5)(0,2t+5)=0$.

Hai thành phố A và B cách nhau 120km. Một ô tô di chuyển từ A đến B, rồi quay trở về A với tổng thời gian đi và về là 4 giờ 24 phút. Tính tốc độ lúc đi của ô tô, biết tốc độ lúc về lớn hơn tốc độ lúc đi là 20%.

Giải các phương trình:

a) $\frac{x+6}{x+5}+\frac{3}{2}=2$;

b) $\frac{2}{x-2}-\frac{3}{x-3}=\frac{3x-20}{(x-3)(x-2)}$.

Cho phương trình $\frac{x}{x-2}=\frac{1}{x+1}+1$.

a) Tìm điều kiện xác định của phương trình đã cho.

b) Xét các phép biến đổi như sau:

$\begin{array}{l}\frac{x}{x-2}=\frac{1}{x+1}+1\\ \frac{x}{x-2}=\frac{x+2}{x+1}\end{array}$

$\frac{x(x+1)}{(x-2)(x+1)}=\frac{(x+2)(x-2)}{(x+1)(x-2)}$

$x^2+x=x^2-4$

$x=-4$

Hãy giải thích cách thực hiện mỗi phép biến đổi trên.

c) $x=-4$ có là nghiệm của phương trình đã cho không?

Tìm điều kiện xác định của mỗi phương trình sau:

a) $\frac{5}{x+7}=\frac{-14}{x-5}$

b) $\frac{3}{3x-2}=\frac{x}{x+2}-1$

Xét hai phương trình

$2x+\frac{1}{x-2}-4=\frac{1}{x-2}(1)$ và $2x-4=0(2)$

a) Có thể biến đổi như thế nào để chuyển phương trình (1) về phương trình (2)?

b) $x=2$ có là nghiệm của phương trình (2) không? Tại sao?

c) $x=2$ có là nghiệm của phương trình (1) không? Tại sao?

Độ cao $h$ (mét) của một quả bóng gôn sau khi được đánh $t$ giây được cho bởi công thức $h=t\left(20-5t\right)$. Có thể tính được thời gian bay của quả bóng kể từ khi được đánh đến khi chạm đất không?

Giải các phương trình:

a) $2x\left(x+6\right)+5\left(x+6\right)=0$;

b) $x\left(3x+5\right)-6x-10=0$.

Giải các phương trình:

a) $\left(x-7\right)\left(5x+4\right)=0$;

b) $\left(2x+9\right)\left(\frac{2}{3}x-5\right)=0$.

Cho phương trình $\left(x+3\right)\left(2x-5\right)=0$.

a) Các giá trị $x=-3,x=\frac{5}{2}$ có phải là nghiệm của phương trình không? Tại sao?

b) Nếu số $x_0$ khác $-3$ và khác $\frac{5}{2}$ thì $x_0$ có phải là nghiệm của phương trình không? Tại sao?

ĐỐ VUI. Chu vi Trái Đất bằng bao nhiêu?

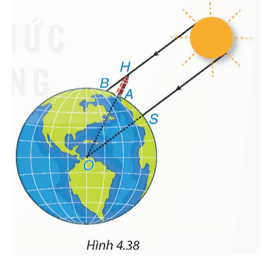
Vào khoảng năm 200 trước Công nguyên, Eratosthenes (Ơ-ra-tô-xten), một nhà toán học và thiên văn học người Hy Lạp, đã ước lượng được 'chu vi' của Trái Đất (chu vi của đường Xích Đạo) nhờ hai quan sát sau:

1. Hồi đó, hằng năm cứ vào trưa ngày Hạ chí (21/6), người ta thấy tia sáng mặt trời chiếu thẳng xuống đáy một cái giếng sâu nổi tiếng ở thành phố Syene (Xy-en), tức là tia sáng chiếu thẳng đứng.

2. Cũng vào trưa một ngày Hạ chí, ở thành phố Alexandria (A-lếch-xăng-đri-a) cách Syene 800 km, Eratosthenes thấy một tháp cao 25 m có bóng trên mặt đất dài 3,1 m.

Từ hai quan sát trên, ông có thể tính xấp xỉ 'chu vi' của Trái Đất như thế nào? (trên Hình 4.38, điểm O là tâm Trái Đất, điểm S tượng trưng cho thành phố Syene, điểm A tượng trưng cho thành phố Alexandria, điểm H là đỉnh của tháp, bóng của tháp trên mặt đất được coi là đoạn thẳng AB).

Cho tam giác ABC vuông tại A, có $\widehat{B}=\alpha$ (H.4.37).

a) Hãy viết các tỉ số lượng giác sinα, cosα.

b) Sử dụng định lí Pythagore, chứng minh rằng sin2α + cos2α = 1.

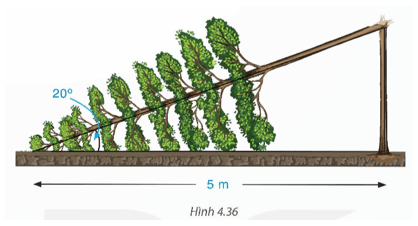
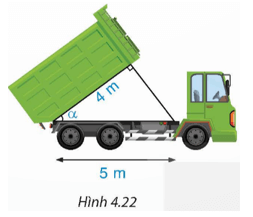
Một cây cao bị gãy, ngọn cây đổ xuống mặt đất. Ba điểm: gốc cây, điểm gãy, ngọn cây tạo thành một tam giác vuông. Đoạn cây gãy tạo với mặt đất góc 20° và chắn ngang lối đi một đoạn 5 m (H.4.36). Hỏi trước khi bị gãy, cây cao khoảng bao nhiêu mét (làm tròn kết quả đến hàng phần mười)?

Hình 4.35 là mô hình của một túp lều. Tìm góc α giữa cạnh mái lều và mặt đất (làm tròn kết quả đến phút).

Xét các tam giác vuông có một góc nhọn bằng hai lần góc nhọn còn lại. Hỏi các tam giác đó có đồng dạng với nhau không? Tính sin và côsin của góc nhọn lớn hơn.

Giá trị tan30° bằng

A. $\sqrt{3}.$

B. $\frac{\sqrt{3}}{2}.$

C. $\frac{1}{\sqrt{3}}.$

D. 1

Với mọi góc nhọn α, ta có

A. sin(90° – α) = cosα.

B. tan(90° – α) = cosα.

C. cot(90° – α) = 1 – tanα.

D. cot(90° – α) = sinα.

Trong tam giác ABC vuông tại A (H.4.34), tan B bằng

A. $\frac{AB}{AC}.$

B. $\frac{AC}{AB}.$

C. $\frac{AB}{BC}.$

D. $\frac{BC}{AC}.$

Trong tam giác MNP vuông tại M (H.4.33), $\sin \widehat{MNP}$ bằng

A. $\frac{PN}{NM}.$

B. $\frac{MP}{PN}.$

C. $\frac{MN}{PN}.$

D. $\frac{MN}{MP}.$

Trong Hình 4.32, cosα bằng

A. $\frac{5}{3}.$

B. $\frac{3}{4}.$

C. $\frac{3}{5}.$

D. $\frac{4}{5}.$

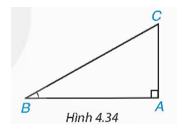
Trong một buổi tập trận, một tàu ngầm đang ở trên mặt biển bắt đầu di chuyển theo đường thẳng tạo với mặt nước biển một góc 21° để lặn xuống (H.4.31).

a) Khi tàu chuyển động theo hướng đó và đi được 200 m thì tàu ở độ sâu bao nhiêu so với mặt nước biển? (làm tròn đến m).

b) Giả sử tốc độ của tàu là 9 km/h thì sau bao lâu (tính từ lúc bắt đầu lặn) tàu ở độ sâu 200 m (tức là cách mặt nước biển 200 m)?

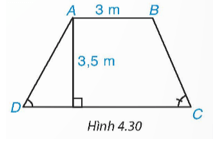
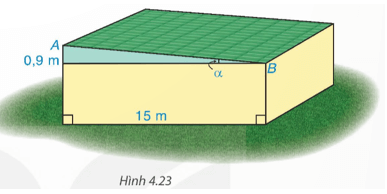
Mặt cắt ngang của một đập ngăn nước có dạng hình thang ABCD (H.4.30). Chiều rộng của mặt trên AB của đập là 3 m. Độ dốc của sườn AD, tức là tanD = 1,25. Độ dốc của sườn BC, tức là tanC = 1,5. Chiều cao của đập là 3,5 m. Hãy tính chiều rộng CD của chân đập, chiều dài của các sườn AD và BC (làm tròn đến dm).

Một bạn muốn tính khoảng cách giữa hai địa điểm A, B ở hai bên hồ nước. Biết rằng các khoảng cách từ một điểm C đến A và đến B là CA = 90 m, CB = 150 m và $\widehat{ACB}=120°$ (H.4.29). Hãy tính AB giúp bạn.

Tính các số liệu còn thiếu (dấu '?') ở Hình 4.28 với góc làm tròn đến độ, với độ dài làm tròn đến chữ số thập phân thứ nhất.

Tìm chiều rộng d của dòng sông trong Hình 4.27 (làm tròn đến m).

Cho tam giác ABC có chân đường cao AH nằm giữa B và C. Biết HB = 3 cm, HC = 6 cm, $\widehat{HAC}=60°.$ Hãy tính độ dài các cạnh (làm tròn đến cm), số đo các góc của tam giác ABC (làm tròn đến độ).

Một cuốn sách khổ 17 × 24 cm, tức là chiều rộng 17 cm, chiều dài 24 cm. Gọi α là góc giữa đường chéo và cạnh 17 cm. Tính sinα, cosα (làm tròn đến chữ số thập phân thứ hai) và tính số đo α (làm tròn đến độ).

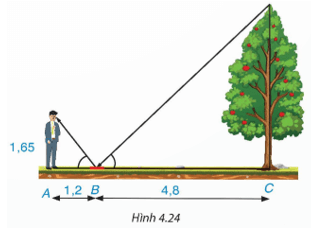
Một người đứng tại điểm A, cách gương phẳng đặt nằm trên mặt đất tại điểm B là 1,2 m, nhìn thấy hình phản chiếu qua gương B của ngọn cây (cây có gốc ở tại điểm C cách B là 4,8 m, B nằm giữa A và C). Biết khoảng cách từ mặt đất đến mắt người đó là 1,65 m. Tính chiều cao của cây (H.4.24).

Cho hình thang ABCD (AD // BC) có AD = 16 cm, BC = 4 cm và $\widehat{A}=\widehat{B}=\widehat{ACD}=90°.$

a) Kẻ đường cao CE của tam giác ACD. Chứng minh $\widehat{ADC}=\widehat{ACE}.$ Tính sin của các góc $\widehat{ADC},\widehat{ACE}$ và suy ra AC2 = AE.AD. Từ đó tính AC.

b) Tính góc D của hình thang.

Tính các góc của hình thoi có hai đường chéo dài $2\sqrt{3}$ và 2.

Tìm góc nghiêng α và chiều rộng AB của mái nhà kho trong Hình 4.23.

Tính góc nghiêng α của thùng xe chở rác trong Hình 4.22.

Giải tam giác ABC vuông tại A có BC = a, AC = b, AB = c, trong các trường hợp:

a) a = 21, b = 18;

b) b = 10, $\widehat{C}=30°;$

c) c = 5, b = 3.

Giải bài toán ở tình huống mở đầu với α = 27° và β = 19°.

Giải tam giác ABC vuông tại A, biết BC = 9, $\widehat{C}=53°.$

Hãy nêu cách giải tam giác ABC vuông tại A khi biết cạnh góc vuông AB (hoặc cạnh huyền BC) và góc B.