Câu hỏi:
182 lượt xema) Chứng minh rằng trong tam giác ABC cân tại A, đường trung trực của cạnh BC là đường cao và cũng là đường phân giác xuất phát từ đỉnh A của tam giác đó.
b) Chứng minh rằng trong tam giác đều, điểm cách đều ba đỉnh cũng cách đều ba cạnh của tam giác
Lời giải
Hướng dẫn giải:
a)
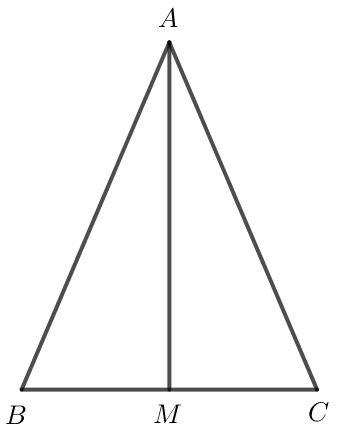
Gọi M là trung điểm của BC.
Khi đó M nằm trên đường trung trực của BC (1)
Do ABC cân tại A nên AB = AC (tính chất tam giác cân)
Do đó A nằm trên đường trung trực của BC (2)
Từ (1) và (2) suy ra AM là đường trung trực của BC nên AM ⊥ BC.
Vì vậy AM là đường cao của tam giác ABC.
Xét ABM và ACM có:
AB = AC (do ABC cân tại A),
AM là cạnh chung
BM = CM (do M là trung điểm của BC),
Do đó ABM = ACM (c.c.c)
Suy ra (hai góc tương ứng)
Nên AM là tia phân giác của góc BAC.
Vậy đường trung trực của cạnh BC là đường cao và cũng là đường phân giác xuất phát từ đỉnh A của tam giác ABC.
b)
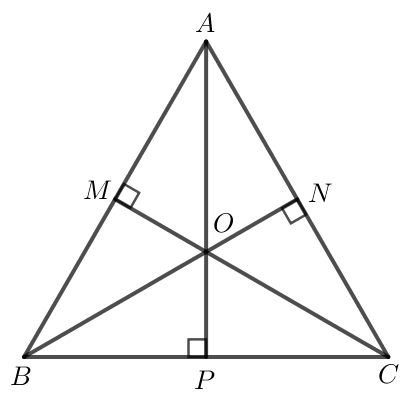
Giả sử ABC đều có O là điểm cách đều ba đỉnh của tam giác đó.
Suy ra O là giao điểm của ba đường trung trực của ABC.
Hay AO, BO, CO lần lượt là đường trung trực của các cạnh BC, AC, AB.
Do ABC đều nên ABC cân tại A.
Do đó theo câu a), ba đường trung trực AO, BO, CO của các cạnh BC, AC, AB lần lượt là đường phân giác xuất phát từ đỉnh A, đỉnh B, đỉnh C của DABC.
Mà ba đường phân giác AO, BO, CO cắt nhau tại O nên O cách đều ba cạnh của tam giác.
Vậy trong tam giác đều, điểm cách đều ba đỉnh cũng cách đều ba cạnh của tam giác.
Chứng minh rằng trong tam giác đều ABC, trọng tâm G cách đều ba đỉnh của tam giác đó
