Câu hỏi:
154 lượt xemXét điểm O cách đều ba đỉnh của tam giác ABC. Chứng minh rằng nếu O nằm trên một cạnh của tam giác ABC thì ABC là một tam giác vuông
Lời giải
Hướng dẫn giải:
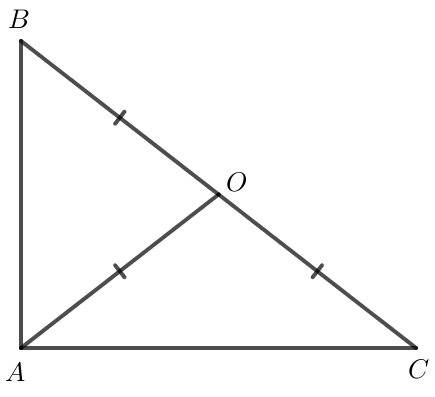
Giả sử O nằm trên cạnh BC của ABC, khi đó OA = OB = OC (do O cách đều ba đỉnh của tam giác).
Vì OA = OB nên OAB cân tại O.
Suy ra, (tính chất tam giác cân).
Vì OA = OC nên OAC cân tại O
Suy ra, (tính chất tam giác cân).
Khi đó hay .
Xét ABC ta có: (tổng ba góc trong một tam giác)
Suy ra
Nên .
Do đó, tam giác ABC vuông tại A.
Vậy nếu O nằm trên một cạnh của tam giác ABC và O cách đều ba đỉnh của tam giác ABC thì ABC là một tam giác vuông.
Chứng minh rằng trong tam giác đều ABC, trọng tâm G cách đều ba đỉnh của tam giác đó
