Câu hỏi:
88 lượt xem Tự luận
Gọi H là trực tâm của tam giác ABC không vuông. Tìm trực tâm của các tam giác HBC, HCA, HAB
Lời giải
Hướng dẫn giải:
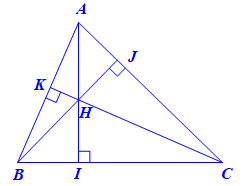
Gọi I, J, K lần lượt là chân đường cao kẻ từ A, B, C đến BC, CA, AB.
Xét DHBC có HI ⊥ BC, CJ ⊥ BH.
Mà HI cắt CJ tại A nên A là trực tâm của HBC.
Xét HCA có HJ ⊥ AC, CI ⊥ AH.
Mà HJ cắt CI tại B nên B là trực tâm của HCA.
Xét HAB có HK ⊥ AB, BI ⊥ AH.
Mà HK cắt BI tại C nên C là trực tâm của HAB.
Câu 1:
Câu 2:
Câu 3:
Câu 4:
Câu 5:
Tự luận
Chứng minh rằng trong tam giác đều ABC, trọng tâm G cách đều ba đỉnh của tam giác đó
1 năm trước
103 lượt xem
Câu 6:
Câu 7:
Câu 8:
Câu 9:
Câu 10:
Câu 12:
Câu 13:
Câu 14:
Câu 15:
