Câu hỏi:
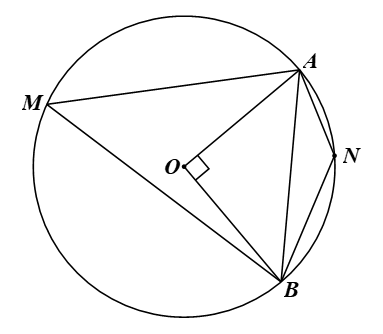
122 lượt xemCho đường tròn (O; R) và dây AB sao cho ˆAOB=90°. Giả sử M, N lần lượt là các điểm thuộc cung lớn AB và cung nhỏ AB (M, N khác A và B).
a) Tính độ dài đoạn thẳng AB theo R.
b) Tính số đo các góc ANB và AMB.
Lời giải
Hướng dẫn giải:
a) Xét đường tròn (O: R) có A, B thuộc đường tròn nên OA = OB = R.
Xét ∆AOB vuông tại O, theo định lí Pythagore, ta có:
AB2 = OA2 + OB2 = R2 + R2 = 2R2.
Do đó: AB = √2R2=R√2.
b) Xét đường tròn (O) có ˆAOB là góc ở tâm chắn cung ANB nên sđANB=ˆAOB=90°.
Ta có: sđAMB=360°−sđANB=360°−90°=270°.
Vì ˆANB^ là góc nội tiếp chắn cung AMB nên ˆANB=12sđAMB=12⋅270°=135°.
Vì ˆAMB^ là góc nội tiếp chắn cung ANB nên ˆAMB=12sđANB=12⋅90°=45°.
Cho đường tròn (O). Hãy vẽ góc xOy có đỉnh là tâm O của đường tròn đó.
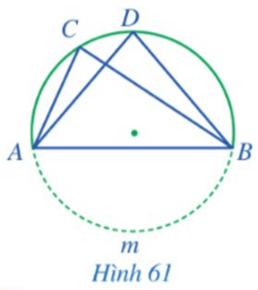
Trong Hình 61, gọi I là giao điểm của AD và BC. Chứng minh IA.ID = IB.IC.