Câu hỏi:
67 lượt xem Tự luận
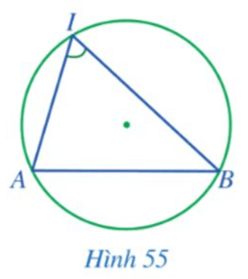
Cho đường tròn (O; R) và dây cung AB = R. Điểm C thuộc cung lớn AB, C khác A và B. Tính số đo góc ACB.
Lời giải
Hướng dẫn giải:
Xét ∆AOB có: OA = OB = AB = R nên ∆AOB là tam giác đều, do đó ˆAOB=60°.
Mà ˆAOB là góc ở tâm và ˆACB là góc nội tiếp cùng chắn cung AB của đường tròn (O). Do đó ˆACB=12⋅ˆAOB=12⋅60°=30°.
Vậy ˆACB=30°.
Câu 1:
Câu 2:
Tự luận
Cho đường tròn (O). Hãy vẽ góc xOy có đỉnh là tâm O của đường tròn đó.
1 năm trước
62 lượt xem
Câu 3:
Câu 4:
Câu 5:
Câu 6:
Câu 7:
Câu 10:
Câu 11:
Tự luận
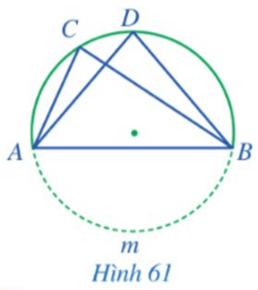
Trong Hình 61, gọi I là giao điểm của AD và BC. Chứng minh IA.ID = IB.IC.
1 năm trước
107 lượt xem
Câu 12:
Câu 13:
Câu 14:
Câu 15:
Câu 16:
Câu 17: