Câu hỏi:
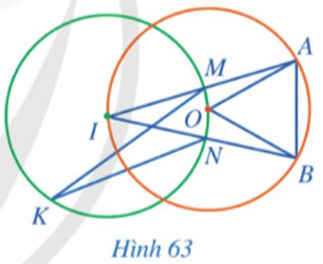
99 lượt xemTrong Hình 63, cho biết AB = OA.
a) Tính số đo góc AOB.
b) Tính số đo cung nhỏ AB và cung lớn AB của (O).
c) Tính số đo góc MIN.
d) Tính số đo cung nhỏ MN và cung lớn MN của (I).
e) Tính số đo góc MKN.
Lời giải
Hướng dẫn giải:
a) Xét ∆OAB có OA = OB = AB nên ∆OAB là tam giác đều, do đó ˆAOB=60°.
b) Số đo cung nhỏ AB là: sđAB=ˆAOB=60°.
Số đo cung lớn AB (cung AIB) là: sđAIB=360°−sđAB=60°−60°=300°.
c) Góc MIN hay chính là góc AIB là góc nội tiếp chắn cung nhỏ AB nên ˆMIN=12sđAB=12⋅60°=30°.
d) Xét đường tròn (I) có góc MIN là góc ở tâm chắn cung nhỏ MN (cung MON) nên số đo cung nhỏ MN là sđMON=ˆMIN=30°.
Số đo cung lớn MN (cung MKN) là:
sđMKN=360°−sđMON=360°−30°=330°.sđ⏜=360°−sđ⏜=360°−30°=330°.
e) Xét đường tròn (I) có góc MKN là góc nội tiếp chắn cung nhỏ MN nên ˆMKN=12sđMN=12⋅30°=15°.
Cho đường tròn (O). Hãy vẽ góc xOy có đỉnh là tâm O của đường tròn đó.
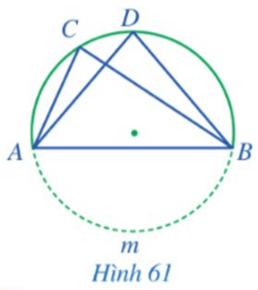
Trong Hình 61, gọi I là giao điểm của AD và BC. Chứng minh IA.ID = IB.IC.